Angle between two lines
Straight Line of Class 11
Acute angle θ between two straight lines with slopes m1 and m2 is given by
tanθ = 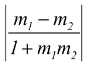 .
.
COR I : If two straight lines in question are parallel to each other then tanθ = 0
⇒ m1 = m2.
II: If they are mutually perpendicular then θ = π/2.
⇒ 1 + m1m2 = 0 or m1m2 = −1
III: two lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are parallel if and only if 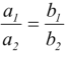 .
.
IV: They are perpendicular if and only if a1a2 + b1b2 = 0.
V: They are coincident if 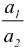 =
= 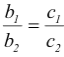 .
.
As an obvious conclusion any line parallel to ax + by + c = 0 is ax + by + k = 0 and perpendicular to ax + by + c = 0 of the form bx − ay + k = 0 where 'k' is a parameter.
Length of perpendicular from a point (x1, y1) on a line.
ax + by + c = 0 is given by 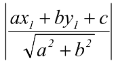 .
.
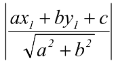 .
.- Introduction
- Expressions for some standard points
- Collinearity of three given points
- Locus and Slope of line
- Equation of Straight line in various forms
- Angle between two lines
- Distance between two parallel lines
- Family of Straight lines
- Exercise 1
- Exercise 2
- Exercise 3(Subjective)
- Exercise 4(Subjective)









