Locus and Slope of line
Straight Line of Class 11
Locus and Slope of line
Locus
Let a point be moving under some constant conditions. Then the path traced by the point is called its locus.
Let (h, k) be the coordinates of the point at any instance. On applying the conditions under which the point is moving, we get some equations involving h, k and some parameters. Eliminate all the parameters to obtain a relation between h and k. Then on replacing h by x and k by y, we get the equation of the locus of the point.
Slope of a Line
Slope or gradient of a line joining two points (x1, y1) and (x2, y2) is denoted conventionally by m = tanθ where θ ≠ π/2 (0 ≤ θ < π) is the angle which the line makes with the positive direction of x-axis and is given by
m =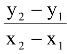 
, where x1≠x2.
- Introduction
- Expressions for some standard points
- Collinearity of three given points
- Locus and Slope of line
- Equation of Straight line in various forms
- Angle between two lines
- Distance between two parallel lines
- Family of Straight lines
- Exercise 1
- Exercise 2
- Exercise 3(Subjective)
- Exercise 4(Subjective)
