Equation of Straight line in various forms

Equation of Straight Line in Various Forms

(a) Equation of a line parallel to x-axis is y = b, where |b| is its distance from
x - axis.

(b) Equation of a line parallel to the y-axis is x = a, where |a| is its distance from
y-axis.

(c) Equation of a line having slope 'm' and an intercept of c units from the y axis is y = mx + c. Note that intercept can be both positive as well as negative.

(d) Equation of a line passing through a fixed point (x₁, y₁) and has a slope equal to m is y - y₁ = m(x − x₁).

(e) Equation of a line passing through two fixed points (x₁, y1) and (x₂, y₂) is
y − y₁ = 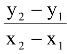(x −x₁), if x1 ≠ x₂.

(f) Let a and b be intercepts made by a straight line on x-axis and y-axis respectively, then the equation of the line in intercept form is 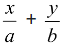 = 1.

(g) Normal form

Let p be the length of perpendicular drawn from the origin to a straight line and let this perpendicular makes an angle α with the positive direction of x-axis. Then the equation of the line is x cosα + y sinα = p.

(h) Parametric form

Let a straight line passes through a fixed point (x1, y1) and makes an angle θ with the positive direction of x-axis. Then equation of the line
is 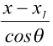= = r(say) where 'r' is a parameter and r ∈ R.

(i) General equation of a straight line is ax + by + c=0 where a and b are not both simultaneously zero.

(ix) Position of Points (x₁, y₁) and (x₂, y₂) relative to a Given Line

Let ax + by + c = 0 be a line. Then two points (x₁, y₁) and (x₂, y₂) are on the same side of the given line if and only if ax₁ + by₁ + c and ax₂ + by₂ + c are of the same sign 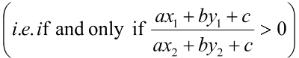and the two points are on the opposite sides of the given line if and only if 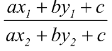< 0.