Family of Straight lines
Straight Line of Class 11
Family of Straight Lines
Any line passing through the point of intersection of L1 = 0 and L2 = 0
(where L1 = a1x + b1y + c1, L2 = a2x + b2y + c2)
is L1 + λL2 = 0, where λ is a parameter.
Concurrent Lines (Lines meeting in a point)
Three lines
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
a3x + b3y + c3 = 0
are concurrent if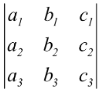 
= 0 or, alternatively if there exists real number α, β, γ not all zero such that αL1 + βL2 + γL3= 0
The image of a point with respect to a straight line Image of the point A(x1, y1) in a line ax + by + c = 0 is B(x, y)
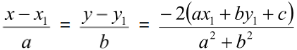
Equation of the angle bisectors of two lines (angle bisector of the lines) a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0
a1b2 ≠ b1a2 and c1 > 0, c2 > 0 are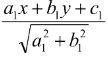 
= ± 
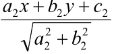
Equation obtained choosing '+' sign is the bisector of the angle containing the origin. Other equation is the equation of the bisector of the angle not containing origin.
If a1a2 + b1b2 > 0 then origin lies in the obtuse angle and if a1a2 + b1b2 < 0, then origin lies in the acute angle.
- Introduction
- Expressions for some standard points
- Collinearity of three given points
- Locus and Slope of line
- Equation of Straight line in various forms
- Angle between two lines
- Distance between two parallel lines
- Family of Straight lines
- Exercise 1
- Exercise 2
- Exercise 3(Subjective)
- Exercise 4(Subjective)
