Expressions for some standard points

Expressions for some standard points

(a) The centroid of a triangle (intersection of medians) with vertices A(x₁, y₁),
B(x₂, y₂) and C(x₃, y₃) is given by x = 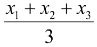and y = .

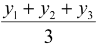(b) The incentre of the triangle (intersection of angle bisectors) ABC is given by

x = 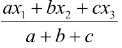y =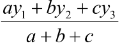

where a, b, c are the lengths of the sides BC, CA and AB of the triangle respectively.

(c) The excentre (center of the ex-circle) touching the side BC is given by

x = 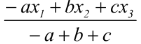y =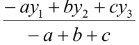

(d) The orthocentre of the triangle ABC is the intersection of altitudes

For a right angled triangle, orthocentre is the point of intersection of base and the perpendicular.

(e) The circumcentre of the triangle ABC is the intersection of the perpendicular bisector of its sides.

The circumcentre of a right angled triangle lies at the mid-point of hypotenuse.

It may be noted here that the orthocentre, the centroid and the circumcentre lie on a straight line and centroid divides the orthocentre and circumcentre in the ratio 2:1 internally.