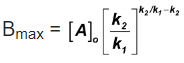Some Complex First Order Reactions

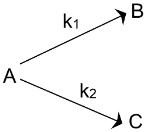
Parallel Reactions:

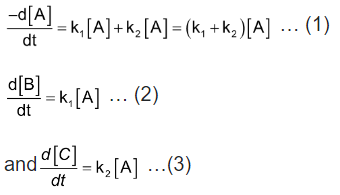
Let us assume that in a time interval, dt, x moles / lit of B was produced and y moles / lit of C was produced.

∴. This means that irrespective of how much time is elapsed, the ratio of concentration of B to that of C from the start (assuming no B and C in the beginning) is a constant equal to k1/k2.

Sequential Reactions:

AB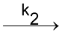C. In this A decomposes to B which in turn decomposes to C.

Integrating equation (1), we get

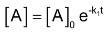
Now we shall integrate equation (2) and find the concentration of B related
to time t.

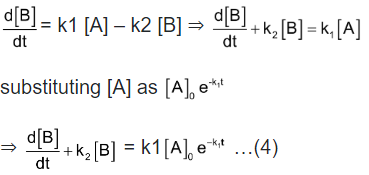
Integration of the above equation is not possible as we are not able to separate the two variables, [B] and t. Therefore we multiply equation (4) by an integrating factor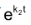, on both the sides of the equation.

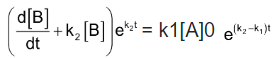
We can see that the left hand side of the equation is a differential of.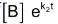

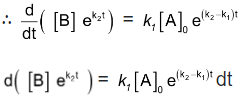
Integrating with in the limits 0 to t.

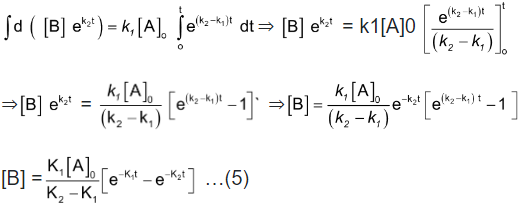
Now in order to find [C], substitute equation (5) in equation (3), we get

On integrating

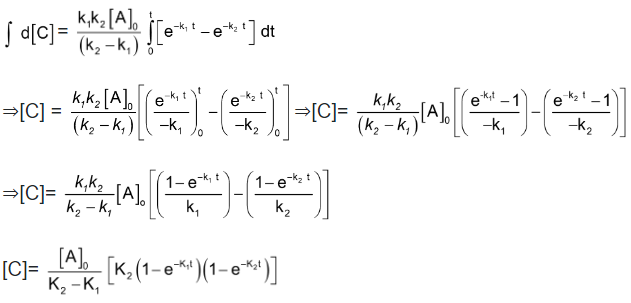
B_max and t_max: We can also attempt to find the time when [B] becomes maximum. For this we differentiate equation (5) and find 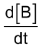& equate it to zero.

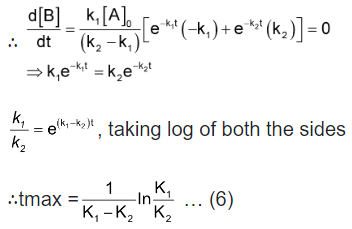
Substituting equation (6) in equation (5)