Rate Of Disintegration And Half-Life Period

The rate of disintegration of a given substance depends upon the nature of disintegrating substance and its total amount. The law of radioactive disintegration may be defined as the quantity of radioactive substance which disappears in unit time is directly proportional to the amount of radioactive substances present or yet not decayed.

The radioactive decay of the different radioactive substances differ widely. The rate of disintegration of a given substance depends upon the nature of disintegrating substance and its total amount. The law of radioactive disintegration may be defined as the quantity of radioactive substance which disappears in unit time is directly proportional to the amount of radioactive substances present or yet not decayed.

Rutherford introduced a constant known as half - life period. It is defined as “time during which half the amount of a given sample of the radioactive substance disintegrates”.

Half life periods vary from billions of years for some radio isotopes to a fraction of a second. Half life period is represented as t1/2. Let the initial amount of a radioactive substance be No. After one half life period (t1/2) it becomes = No/2. After two half life periods (2t1/2) it becomes = No/4 and after n half life periods (nt1/2) it becomes = (1/2)ⁿ N₀. Thus, for the total disintegration of a radioactive substance an infinite time will be required.

Amount of radioactive substance left after n half life periods N = (1/2)ⁿ N₀ and total time T = n × t1/2. Where n is a whole number.

Disintegration constant: A chemical reaction whose rate varies directly to the concentration of one molecular species only, is termed as first order reaction. Radioactive disintegration is similar to such a chemical reaction as one radioactive species changes into other. This can be represented as.

A → B

Suppose the number of atoms of a radioactive substance present at the start of observation, i.e., when t = 0, is No and after time t the number of atoms remaining unchanged is N. At this instant of very small number of atoms dN disintegrate in a small time dt; the rate of change of A into B is given -dN/dt. The negative sign indicates the number of atoms decreases as time increases.

Since rate of disintegration or change is proportional to the number of atoms present at that time, the relation becomes.

-dN/dt = λ.N …(i)

'λ' is called the disintegration constant or decay constant.

Evidently, -dN/N = λ.dt …(ii)

If dt = 1 second, λ =-dN/N … (iii)

Thus, λ may be defined as the fraction of the total number of atoms which disintegrates per second at any time.

Integrating equation (ii),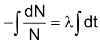
or, – log N = λt + C ……… (iv)

where C is the integration constant.

When t = 0, N = N0

Putting values in equation (iv)

– log N₀ = C

Putting the value of C in equation (iv)

– log N = λt – log N₀

or, log N_o – log N = λt

or, log 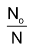= λt

or, 2.303 log₁₀ 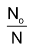= λt

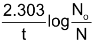or, λ = … (v)

This equation is called kinetic equation and is obeyed by first order reactions.

Relationship between half life period and radioactive disintegration constant

When t = t1/2 N =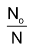

Putting the values in equation (v)

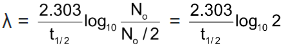
So, λ = [ log10² = 0.3010]

or, t1/2 =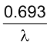

Thus, half life period of a given radioactive substance does not depend on the initial amount of a radioactive substance but depends only on the disintegration constant of the radioactive element.

Average life Period (T)

Since total decay period of any element is infinity, it is meaningless to use the term total decay period for radioelement. Thus the term average life is used which is determined by the following relation.

Average life (T) =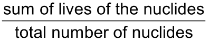

Relation between average life and half - life

Average life(T) of an element is the inverse of its decay constant, i.e.,

T =

Substituting the value of λ =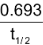

Average life (T) = 1.44 × Half life (t1/2)