Bomb Calorimeter

The bomb calorimeter used for determining change in internal energy at constant volume if reaction for the combustion is known than enthalpy of combustion can be estimated by using formula
ΔH = ΔE + ΔnRT.

This apparatus was devised by Berthelot (1881) to measure the heat of combustion of organic compounds. A modified form of the apparatus shown in Figure consists of a sealed combustion chamber, called a bomb, containing a weighed quantity of the substance in a dish alongwith oxygen under about 20 atm pressure. The bomb is lowered in water contained in an insulated copper vessel. This vessel is provided with a stirrer and a thermometer reading up to 1/100th of a degree. It is also surrounded by an outer jacket to ensure complete insulation from the atmosphere. The temperature of water is noted before the substance is ignited by an electric current. After combustion, the rise in temperature of the system is noted on the thermometer and heat of combustion can be calculated from the heat gained by water and the calorimeter. By knowing the heat capacity of calorimeter and also the rise in temperature, the heat of combustion can be calculated by using the expression

Heat exchange = Z × ΔT

Z–Heat capacity of calorimeter system

ΔT– rise in temp

Heat changes at constant volumes are expressed in ΔE and Heat changes at constant pressure are expressed in ΔH. Also, ΔH = ΔE + ΔnRT

Δn = gaseous product moles – gaseous reactant moles.

Application of bond energies

(i) Determination of enthalpies of reactions

Suppose we want to determine the enthalpy of the reaction.

If bond energies given for C ⎯ C, C = C, C⎯H, and H ⎯ H are 347.3, 615.0, 416.2 and
435.1KJ mol−1 respectively.

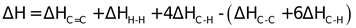
= (615.0 + 435.1) − (347.3 + 832.4) ⇒ −129.6 KJ

(ii) Determination of enthalpies of formation of compounds

Consider the formation of acetone.

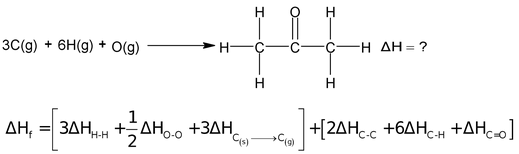
by putting the value of different bond energies you can determine the ΔHf.

(iii) Determination of resonance energy

If a compound exhibits resonance, there is a considerable difference between the enthalpies of formation as calculated from bond energies and those determined experimentally. As an example we may consider the dissociation of benzene.

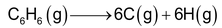
Assuming that benzene ring consists of three single and three double bonds (Kekule’s structure) the calculated dissociation energy comes out to be 5384.1 KJ from bond energies data.

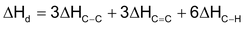
The experimental value is known to be 5535.1 KJ/mol. Evidently, the energy required for the dissociation of benzene is 151 KJ more that the calculated value. The difference of 151 KJ gives the resonance energy of benzene.