Lattice Energy Of An Ionic Crystal (Born–Haber Cycle)

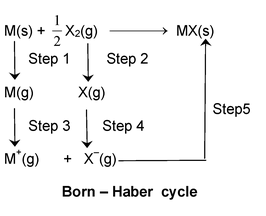
The change in enthalpy that occurs when 1 mole of a solid crystalline substance is formed from its gaseous ions, is known as Lattice energy.

Step 1: Conversion of metal to gaseous atoms

M(s) → M(g) , ΔH1 = sublimation

Step 2: Dissociation of X₂ molecules to X atoms

X2(g) → 2X (g), ΔH₂ = Dissociation energy

Step 3: Conversion of gaseous metal atom to metal ions by losing electron

M(g) → M+ (g) + e–, ΔH3 = (Ionization energy)

Step 4: X(g) atoms gain an electron to form X– ions

X(g) + e– → X–(g), ΔH4 = Electron affinity

Step 5: M+ (g) and X– (g) get together and form the crystal lattice

M+ (g) + X– (g) → MX(s) ΔH5 = lattice energy

Applying Hess’s law we get

ΔH₁ + 1/2 ΔH₂ + ΔH₃ + ΔH₄ + ΔH₅ = ΔHf (MX)

On putting the various known values, we can calculate the lattice energy.