Graphical Interpretation of Displacement, Velocity And Acceleration
Kinematics of Class 11
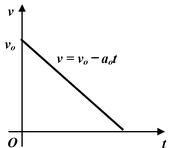
Average Velocity
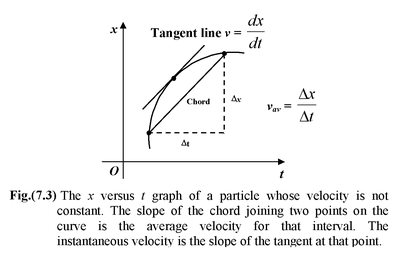
The average velocity between two points in a given time interval can be obtained from a displacement versus time graph by computing the slope of the straight line joining the coordinates of the two points.
Instantaneous Velocity
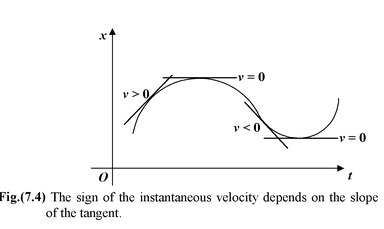
The instantaneous velocity at time t is the slope of the tangent line drawn to the position−versus−time graph at that time.
|
|
|
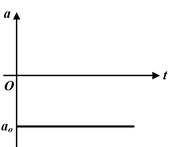
Average Acceleration
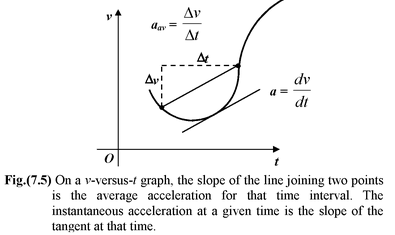
The average acceleration between two points in a time interval is equal to the slope of the chord connecting the points on a velocity versus time graph.
Instantaneous Acceleration
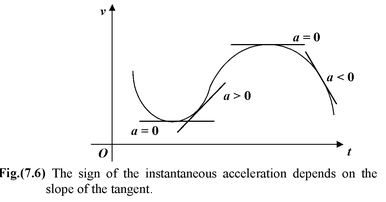
The instantaneous acceleration at time t is the slope of the tangent drawn to the velocity versus time graph.
|
|
|
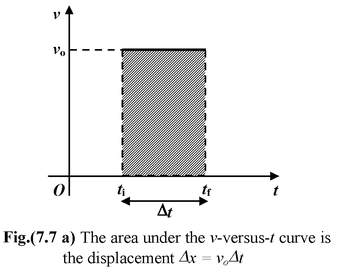
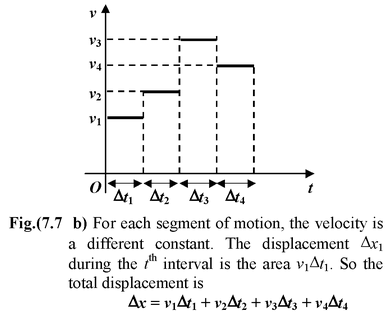
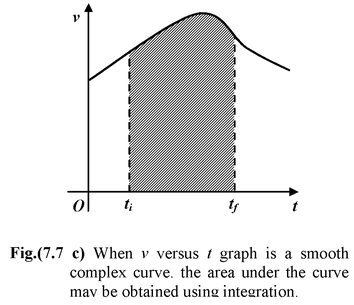
Displacement from Velocity Time GraphsGiven a velocity versus time graph, the displacement during an interval between time ti and tf is the area bounded by the velocity curve and the two vertical lines t = ti and t = tf, as shown in the Fig.(7.7 a). |
|
|
|
|
Velocity from Acceleration Time Graphs
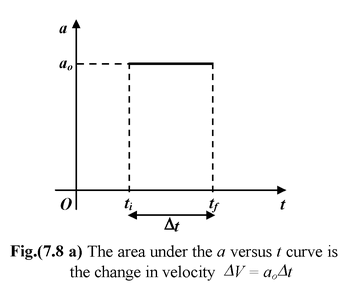
Given an acceleration−versus−time graph, the change in velocity between t = ti and t = tf is the area bounded by the acceleration curve and the vertical lines t = ti and t = tf.
|
|
|
Table 7.1 Variation of Displacement (x), velocity (v) and acceleration (a) with respect to time for different types of motion.
|
Displacement |
Velocity |
Acceleration |
|
|
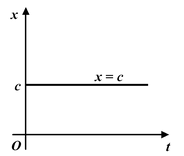
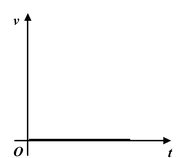
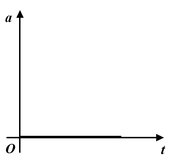
1. At rest |
|
|
|
|
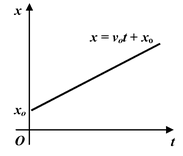
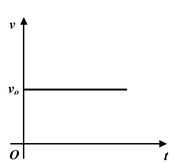
2. Motion with constant velocity |
|
|
|
|
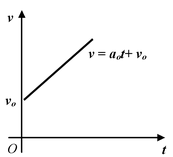
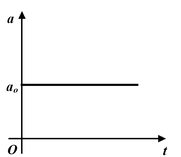
3. Motion with constant acceleration |
|
|
|
|
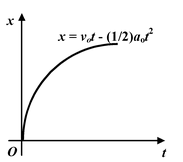
4. Motion with constant deceleration. |
|
|
|
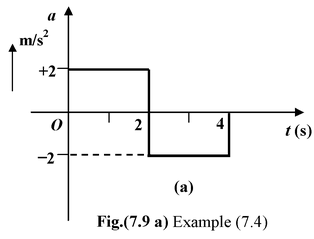
Example: 7.4
|
At t = 0 a particle is at rest at the origin. Its acceleration is 2 m/s2 for the first 2 second and −2 m/s2 for the next 2 s. Plot the Solution
It is given that x = 0 and v = 0 at t = 0. The acceleration versus time graph is plotted in Fig. (7.9a). The velocity at t = 2 s is equal to the sum of velocity at t = 0 and the area under the acceleration−time graph between |
|
v2 = v0 + 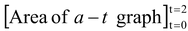
Since at t = 0: velocity is zero, vo = 0
∴ v2 = 0 + (2) (2) = 4 m/s
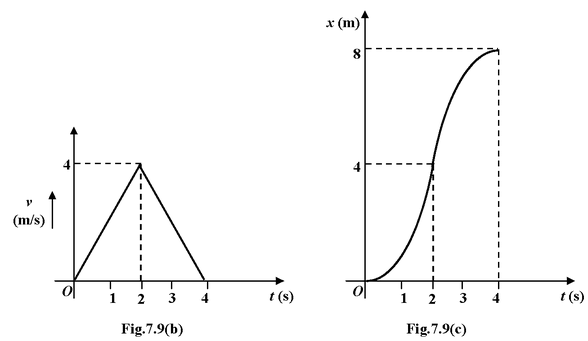
Similarly velocity at t = 4s is
v4 = v0 +  = 0 +2 (+2) + 2 (−2) = 0
= 0 +2 (+2) + 2 (−2) = 0
Note that area below the x−axis is taken as negative
The displacement at t = 2 s is
x2 = x0 + 
∴ x2 = 0 + 1/2 (2) (4) = 4 m
and x4 = 0 + 1/2 (4) (4) = 8 m