Motion With Constant Acceleration
Kinematics of Class 11
In this section, we are going to derive equations relating to displacement, velocity, acceleration and time.
We know that,dv/dt = a
or dv = adt
On integrating both sides,we get
∫dv= ∫adt
v = at + c1where c1= constant of integration
If v0be the initial velocity of the particle then at t = 0, v= v0. This implies that c1= v0
v= v0+ at(7.5)
Also we know that
dx/dt = v = vo + at
ordx = (v0+ at)dt
On integrating, we get
∫dx = ∫v0dt+ ∫atdt
x = v0t + 1/2 at2+ c2 where c2= constant
If x0be the initial position of the particle, then at t = 0; x = x0. This implies that c2= x0
x = x0+ v0t+ 1/2 at2(7.6)
Eliminating t from equations (7.5)and (7.6), we get
v2= vo2 + 2a(x - xo) (7.7)
The equations (7.5) to (7.8) are called the equations of kinematics in the direction along the x−axis.
The equations of kinematics are summarised as
v = v0+ at(7.5)
x = x0+ v0t + 1/2 at2(7.6)
v2= vo2 + 2a(x - xo)(7.7)
x = x0+ 1/2 (v0+ v)t(7.8)
where x0= Initial position coordinate
x = Final position coordinate
v = Final velocity
a = Acceleration (constant)
t = Elapsed time
Problem Solving Strategy1.Make a simple sketch of the situation described 2.Set up a co−ordinate system and clearly indicate the origin. 3. (a)List the given quantities with appropriate signs. (b)List the unknown quantities.
4.Find the equation that has the quantity you need as the only unknown. (This is not always 5.It is often helpful to obtain a rough graphical solution 6.Solve the equation (s) to find the desired unknown(s). |
Example 7.5
A car accelerates with a constant acceleration from rest to 30 m/s in 10 s. It then continues at a constant velocity. Find
(a)its acceleration
(b) how far it travels while speeding up
(c)the distance it covers while its velocity changes from 10 m/s to 20 m/s
Solution
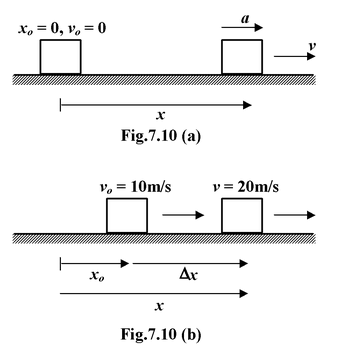
A sketch and coordinate system are shown in figure(a). Note that x0= 0
(a)Given
v0= 0; v = 30 m/s; t = 10s
Unknown:
a= ? x = ?
|
From equation (7.5)we have a= v - vo/t = +3 m/s2 (b)Given : v0= 0; v = 30 m/s; t = 10 s; a= 3 m/s2 Unknown: x= ? The position coordinate x appears as the only unknown in equations (7.6) and (7.8). x= 1/2 at2= 1/2(3) (10)2= 150 m If we had not found the acceleration in (a), we would have to use equation (7.8). x = x0+ 1/2(v0+ v) t = 0 + 1/2(0 + 30) (10) = 150 m (c)Given: v0= 10 m/s; v = 20 m/s; a = 3 m/s2 Unknown : x0= ?; x = ?; t = ? |
|
If we maintain the origin as shown in figure, we have to find x0to this part of the trip. However, we need only the difference Δx= x −x0, which can be found from equation (7.7).
v2= vo2 + 2aΔx
202= 102+ 2(3)Δx
Δx= 50 m
Example 7.6
A particle is at x= 5 m at t =2 s and has a velocity v = 10 m/s. Its acceleration is constant at −4 m/s2. Find the initial position at t = 0
Solution
Given x = 5 m; v = 10 m/s ; a = −4 m/s2; t =2 s
Unknown: x0= ?; v0= ?
In this case none of the equations of kinematics yields x0immediately. The quantity x0appears in three equations, but always with the other unknown, v0. We have to find v0first, From equation (7.5).
v = v0+at
10 = v0+ (−4) (2)
Thus v0= 18 m/s. Any of the other equations will give x0. From equation (7.8).
x = x0+ 1/2 (v0+ v)t
5 = x0+ 1/2 (18 +10) (2)
Thus, x0= −23 m

Example 7.7
Car Amoves at a constant velocity 15 m/s. Another car Bstarts from rest just as the car Apasses it . The car Baccelerates at 2 m/s2until it reaches its maximum velocity of 20 m/s. Where and when does the car Ais caught by other car B?
Solution
When two particles are involved in the same problem, we use simple subscripts to distinguish the variables, as shown in figure. The motion of the car Bhas two phases: one at constant acceleration and other at constant velocity. In such problems it is convenient to use Δtinstead of tin the equations. The car Bmay or may not catch the car Aduring the acceleration phase. This has to be checked. We set the origin at the car B, which means xoA= xoB= 0
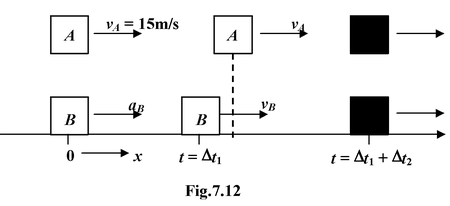
Acceleration Phase:
Let it takes a time interval Δt1
Given: vA= 15 m/s; aB=2 m/s2; v0B = 0; vB= 20 m/s
Unknown: xA= ?; xB= ?
vB= vOB+ aBt
∴t = vB/aB = 20/2 = 10 s
At this time, the positions are given by x= x0+ v0t + 1/2 at2
xA = (15) (10) = 150 m
xB= 1/2(2) (10)2100 m
The car A is still ahead
Constant velocity phase:
Let it take a time interval Δt2
Given: xoA= 150 m; xoB =100 m; vA= 15 m/s; vB= 20 m/s. aA= aB=0
Unknown: xA= ?; Δt2= ?
The cars meet when they have same position
xA= xB
Here xA= 150 + 15 (Δt2)
xB= 100+ 20 (Δt2)
∴150 + 15 (Δt2) = 100 + 20 (Δt2)
orΔt2= 10 s
Also,xA= xB= 300 m