HOW TO FIND CUBE ROOT OF A GIVEN NUMBER
Cubes and Cube Root of Class 8
CUBE ROOT THROUGH A PATTERN:
First Pattern:
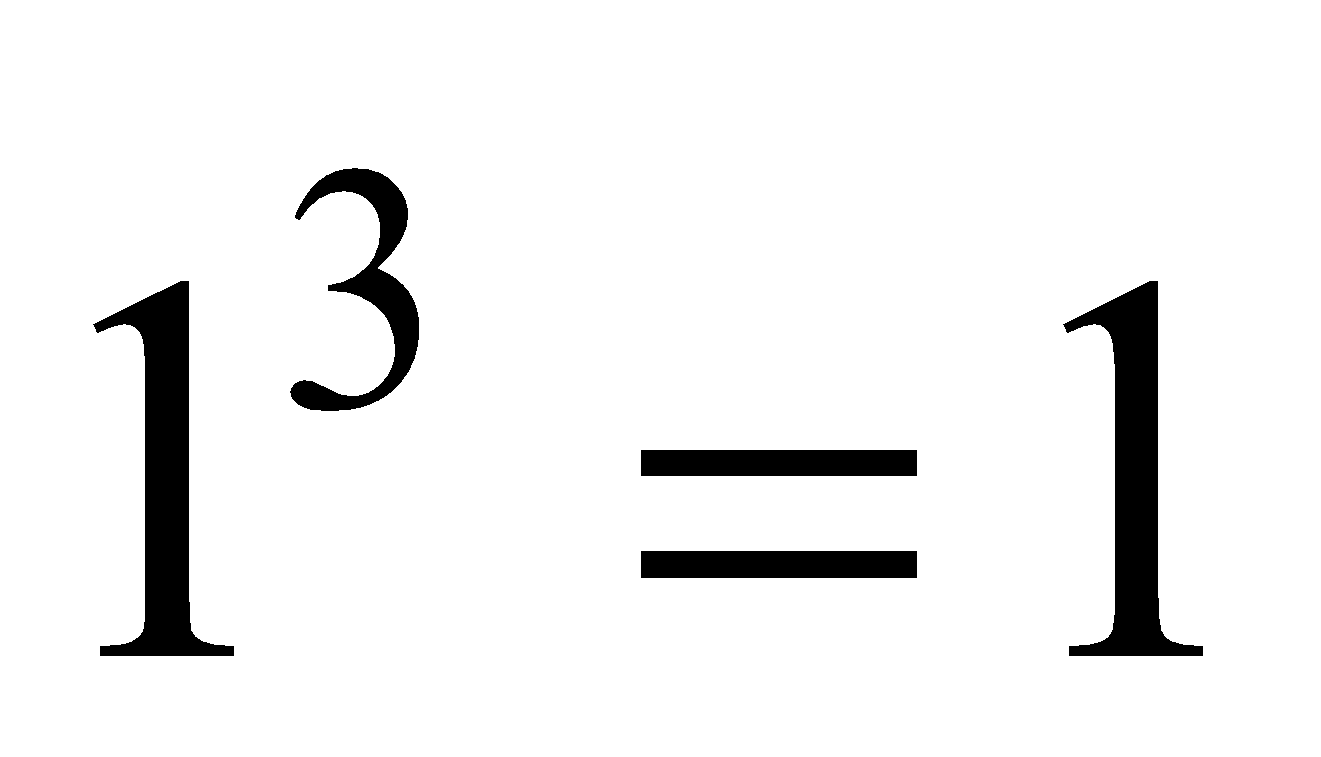
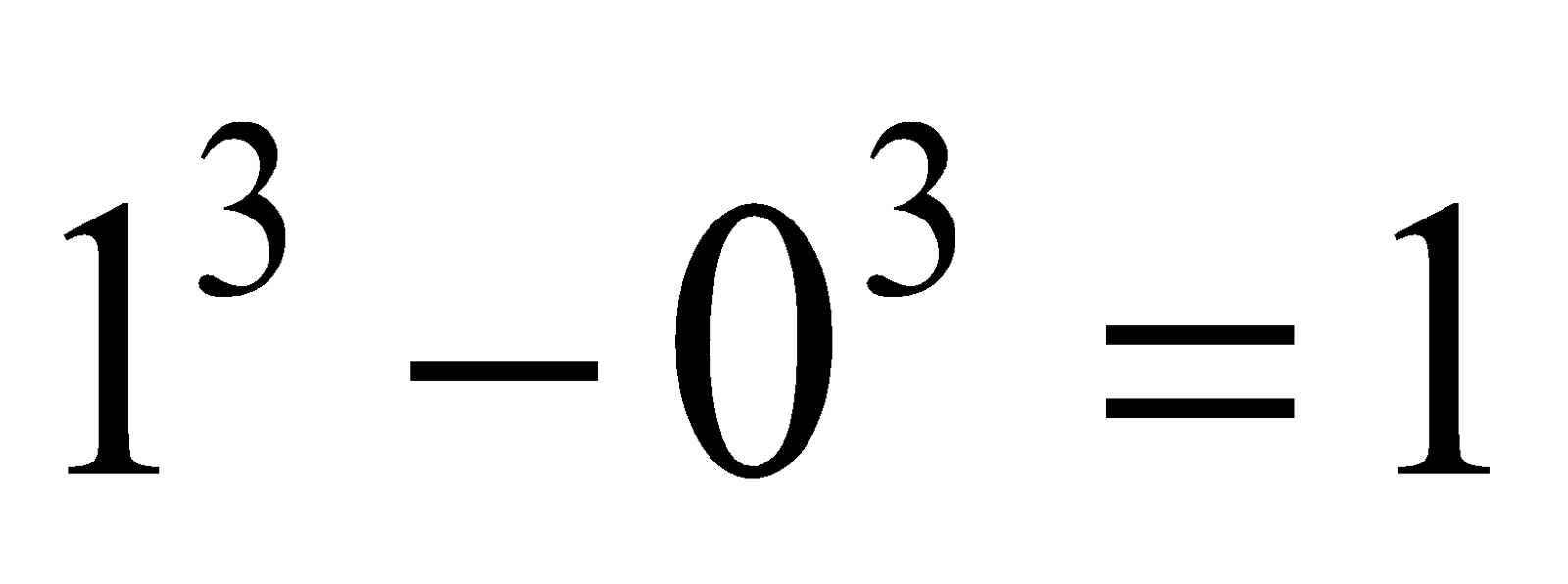

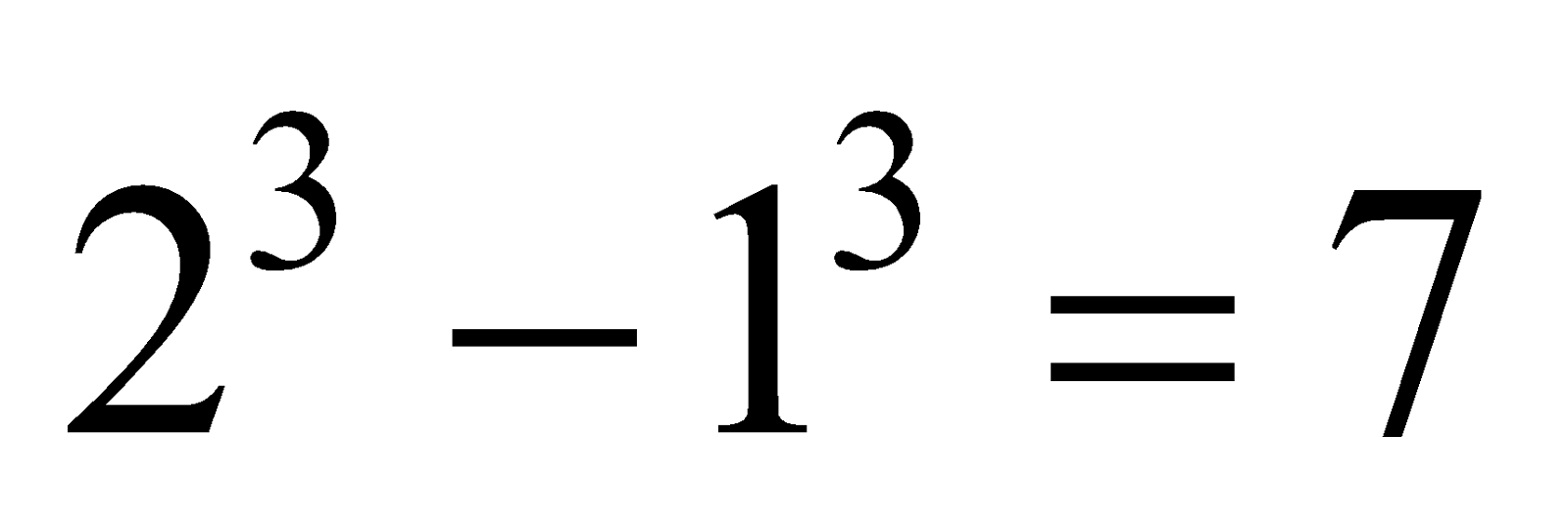 also 1 + 7 =
also 1 + 7 =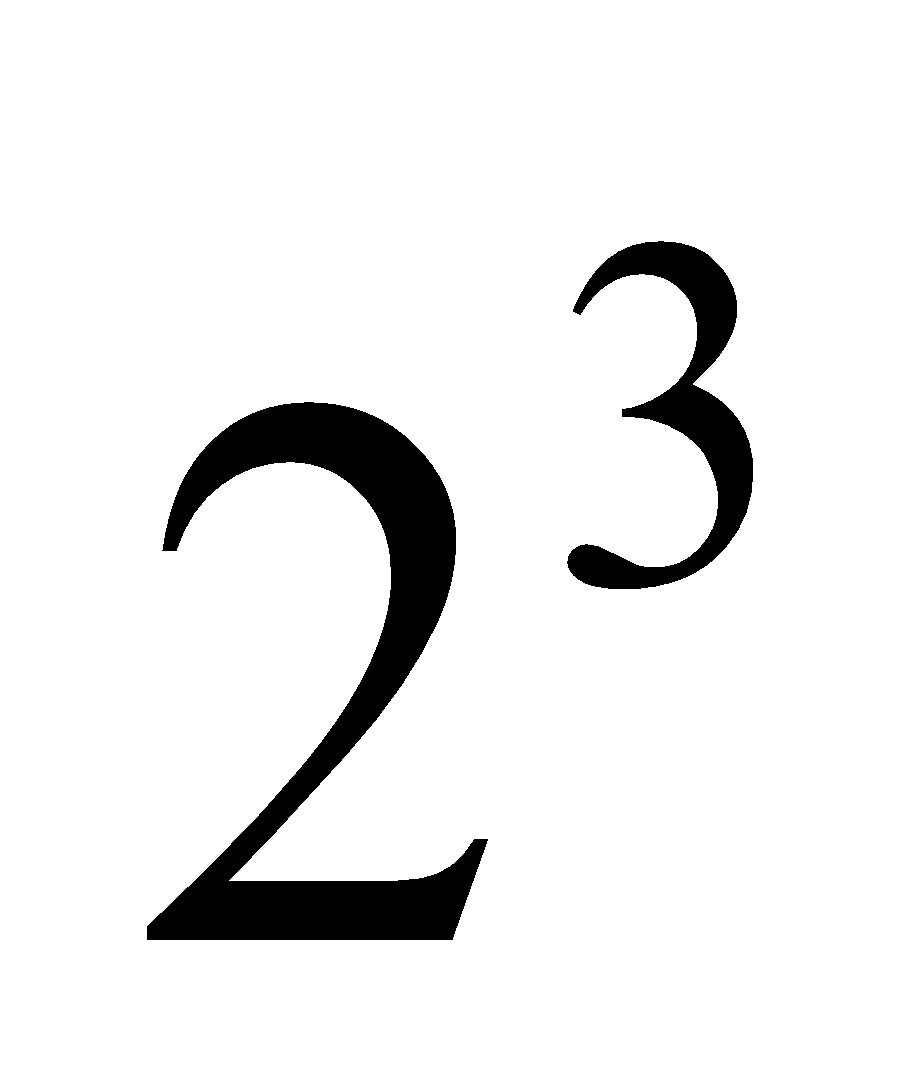
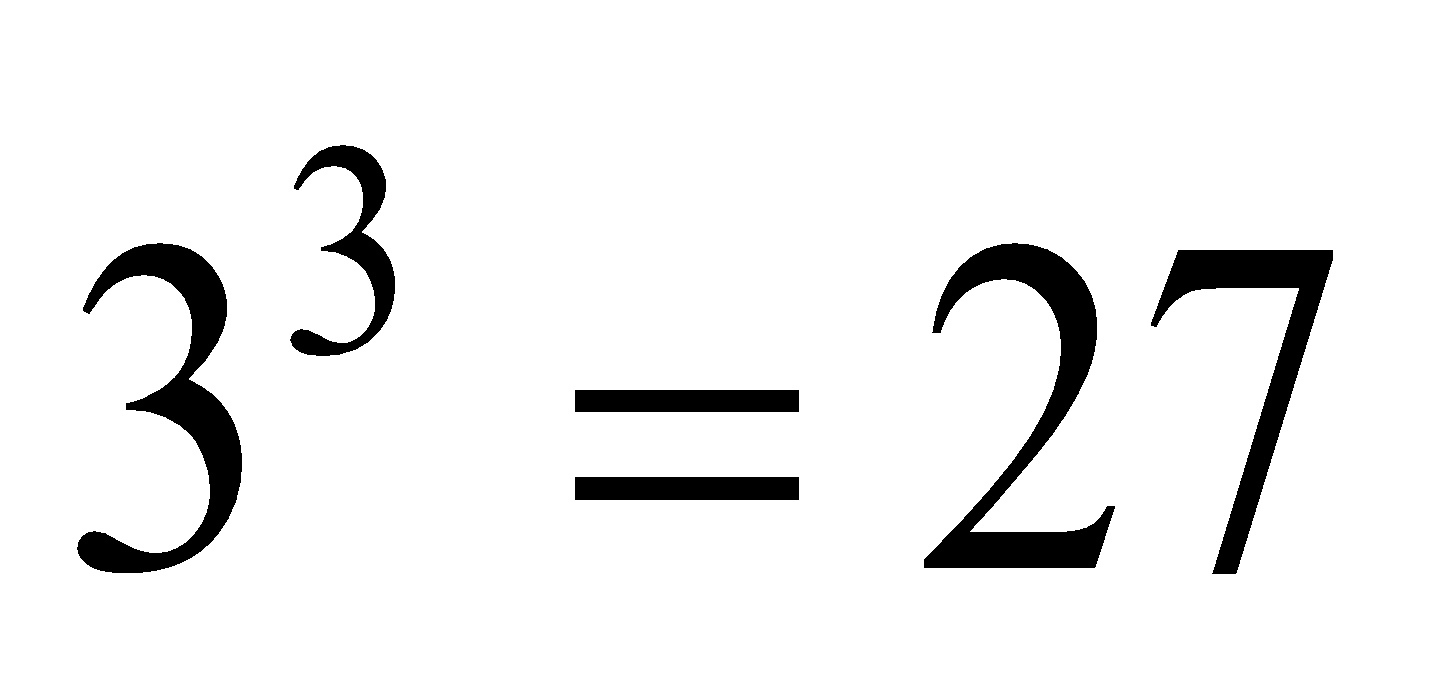
 also 1 + 7 + 19 =
also 1 + 7 + 19 = 

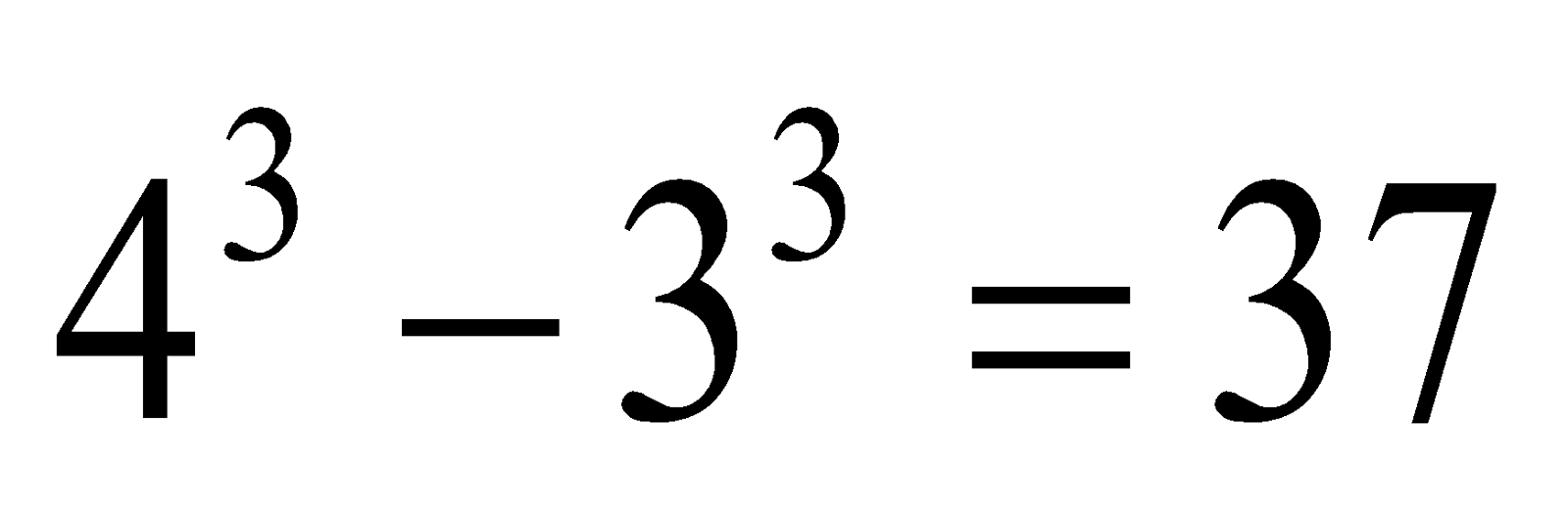 also
also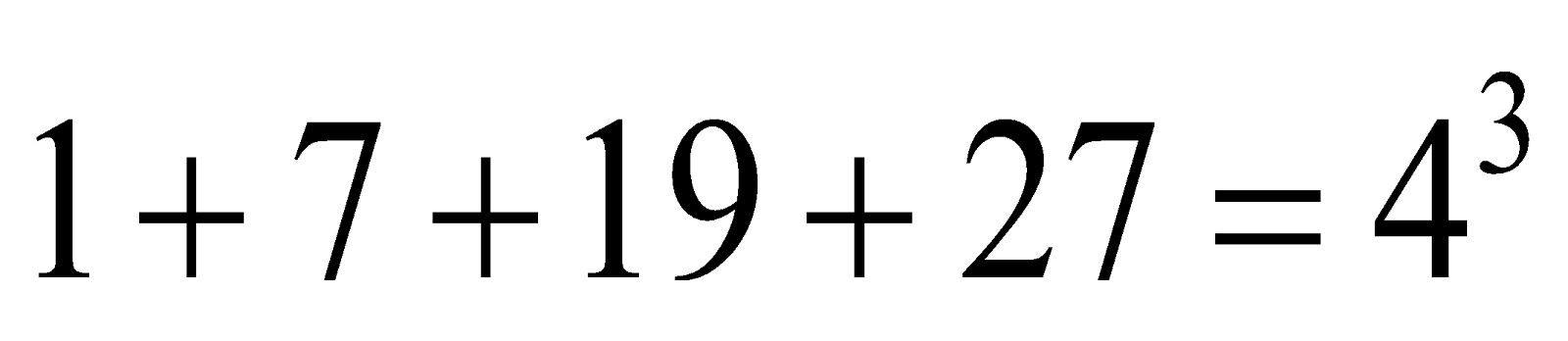

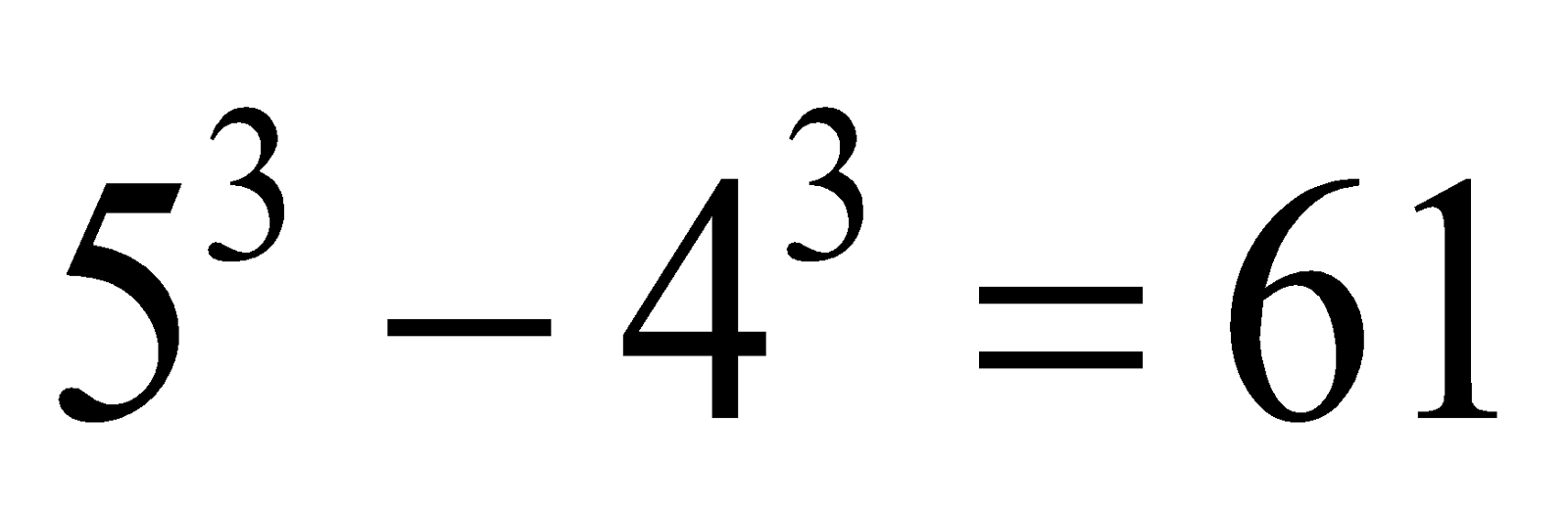 also 1 + 7 + 19 + 37 + 61 =
also 1 + 7 + 19 + 37 + 61 = 
Second Pattern:
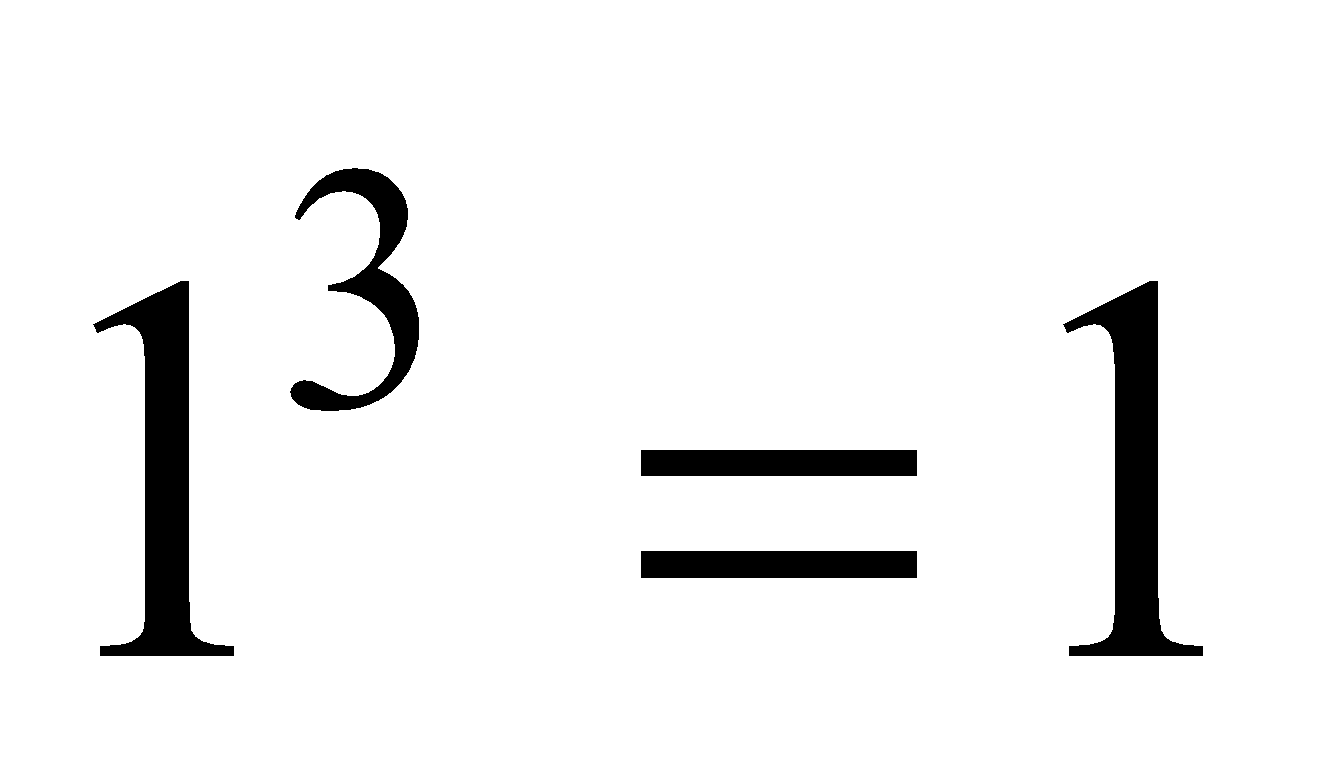
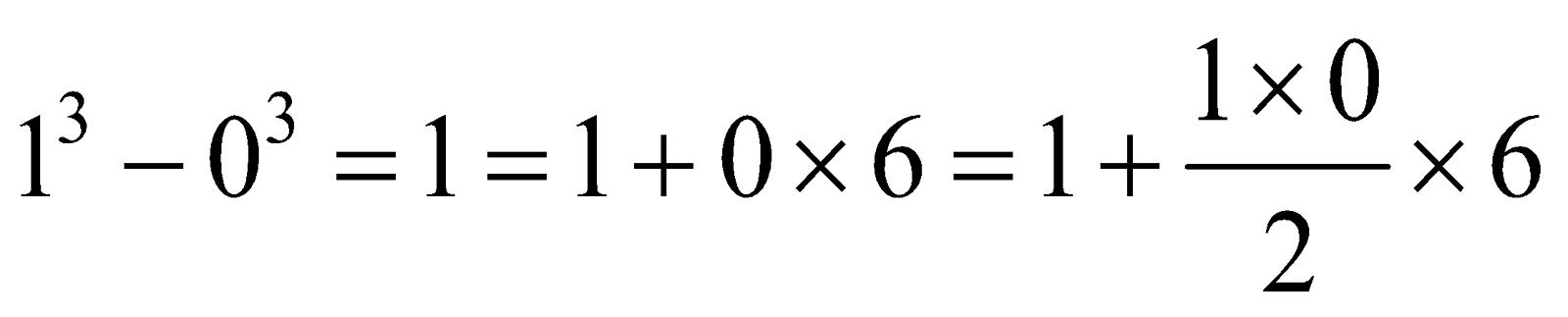
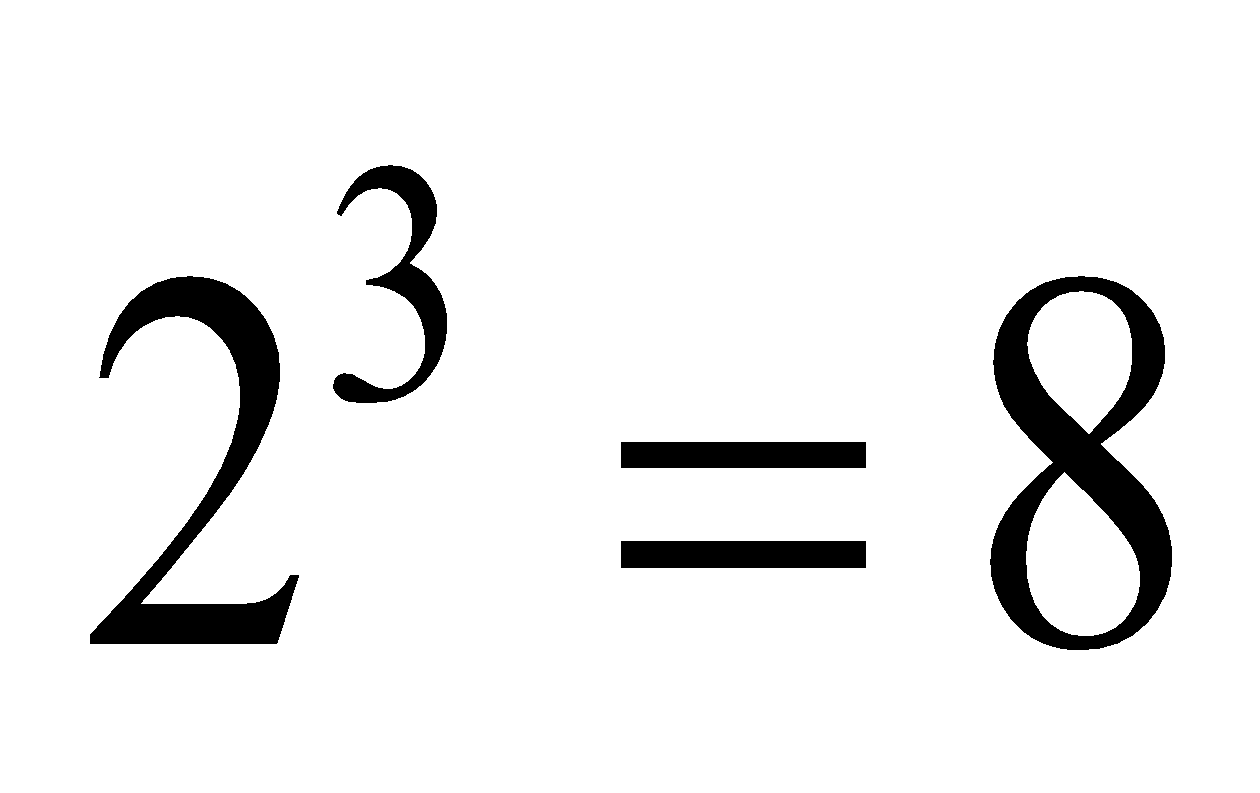
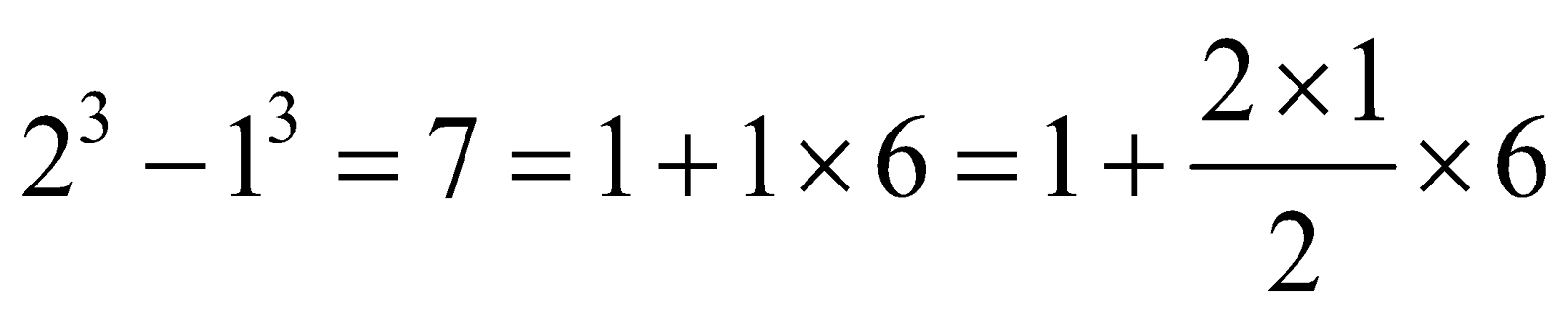
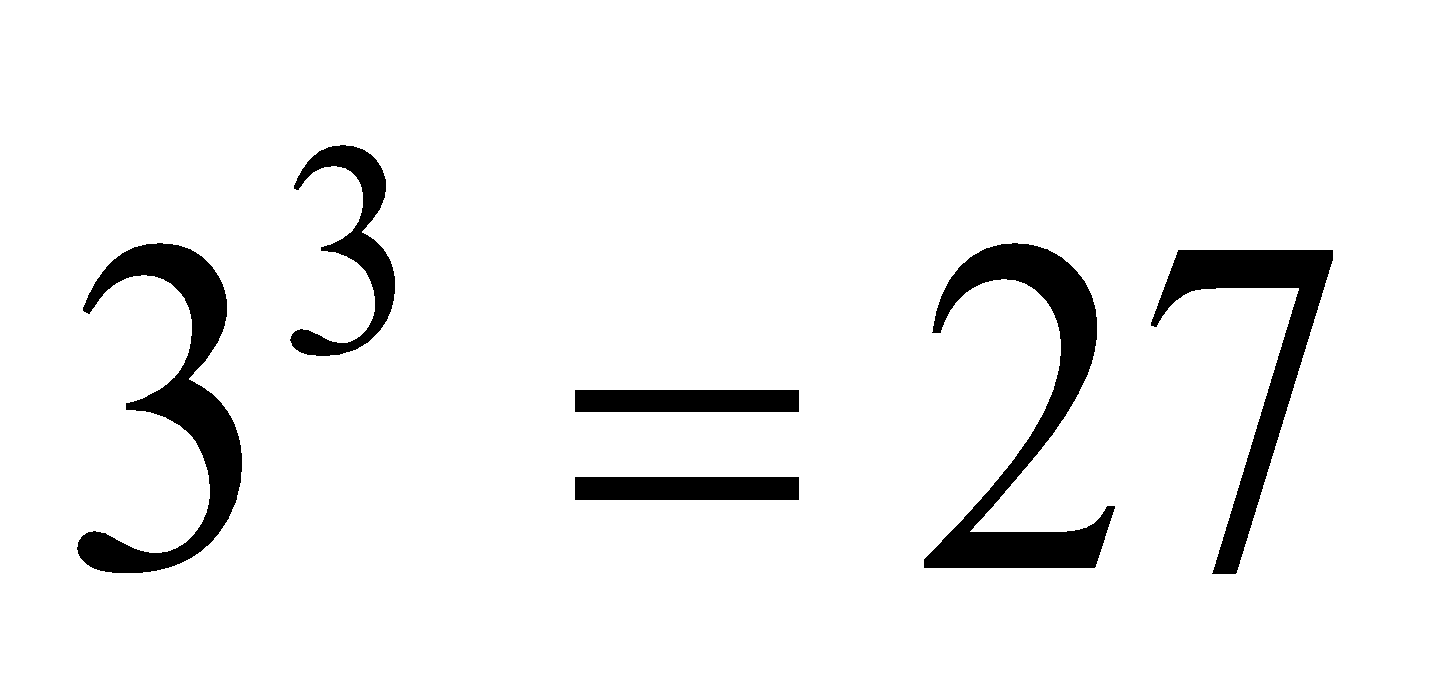
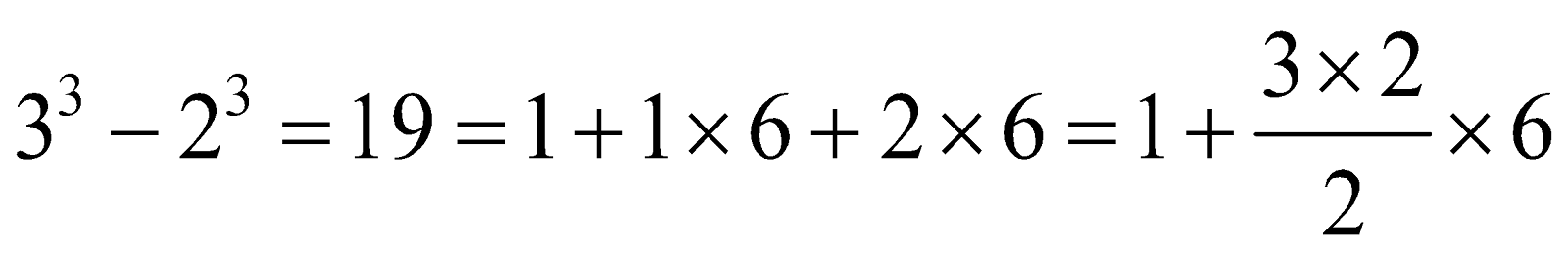
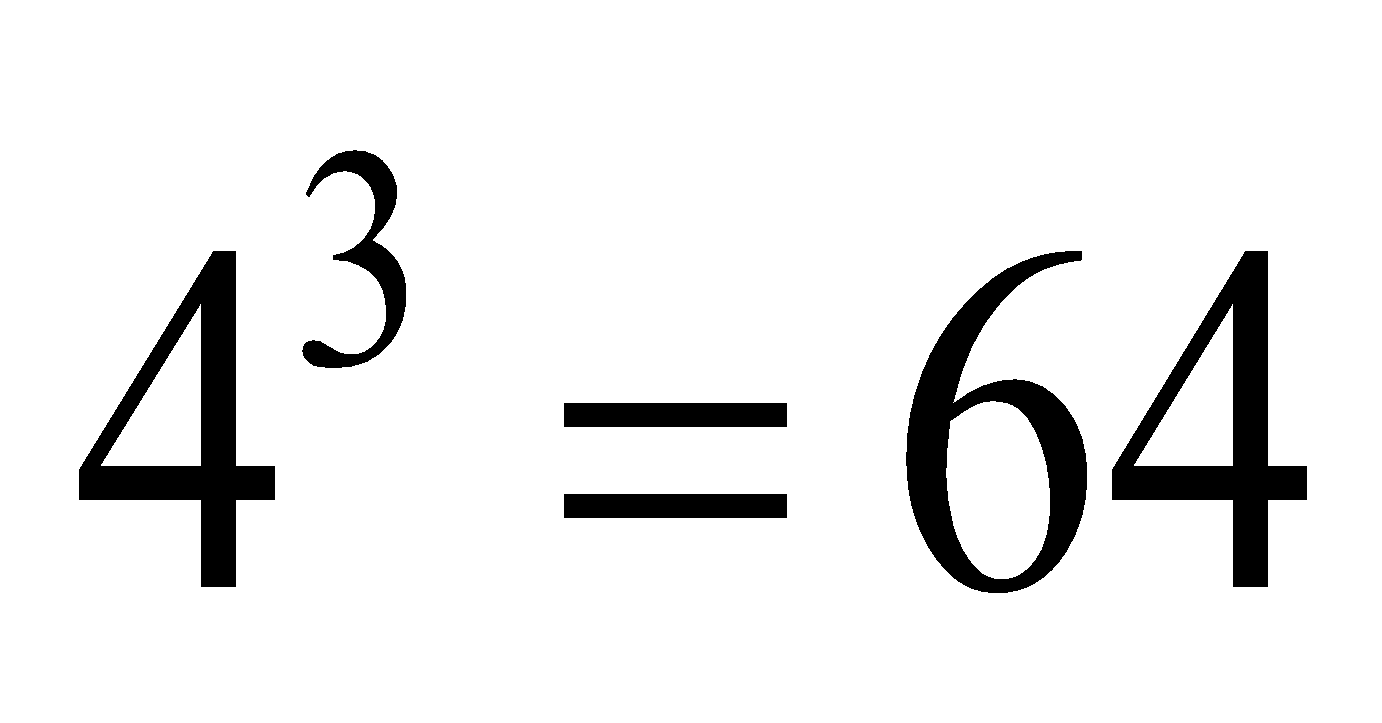
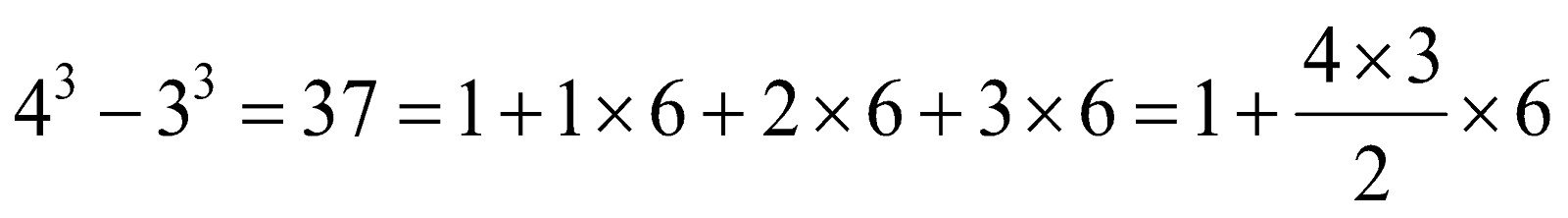

.png)
Thus,

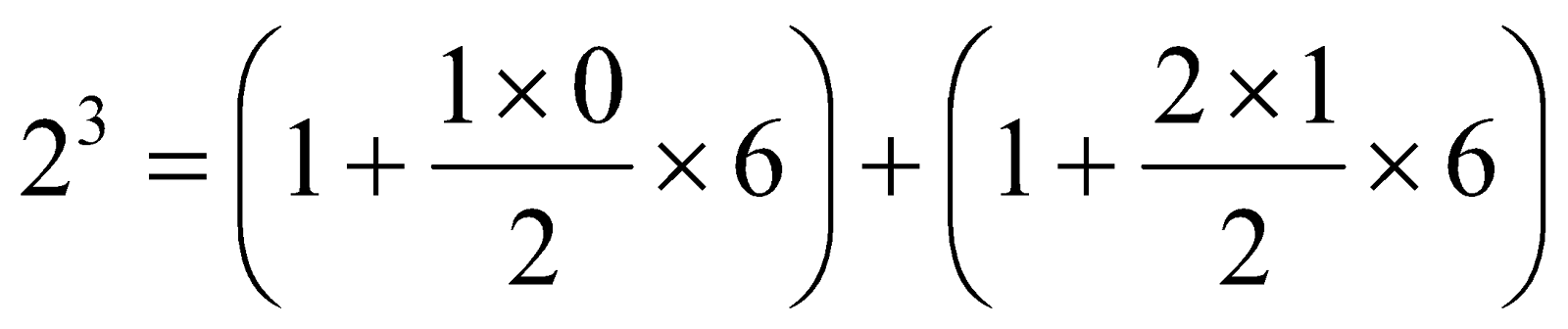
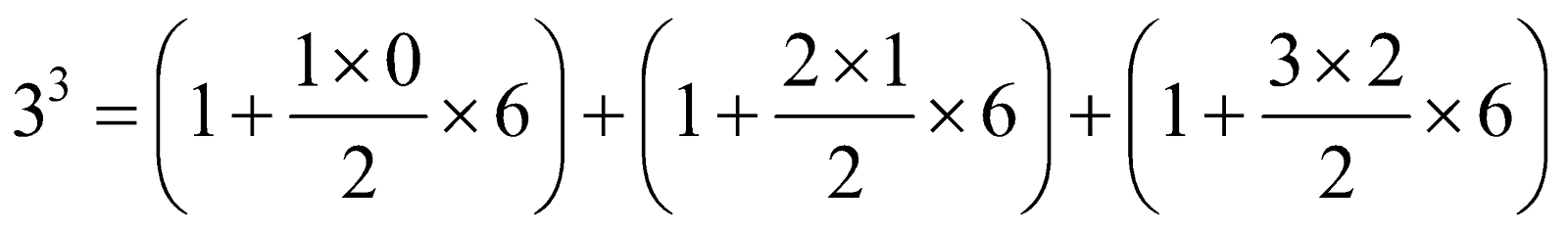 and so on.
and so on.
CUBE ROOT USING UNIT’S DIGIT:
- The cube of a number ending in 0, 1, 4, 5, 6 and 9 ends in 0, 1, 4, 5, 6 and 9 respectively.
- The cube of a number ending in 2 ends in 8 and vice-versa.
- Similarly, the cube of a number ending in 3 or 7 ends in 7 or 3 respectively.
Thus, by looking at the unit’s digit of a perfect cube number, we can find the unit’s digit of the cube-root.
CUBE ROOT BY PRIME FACTORIZATION
To find 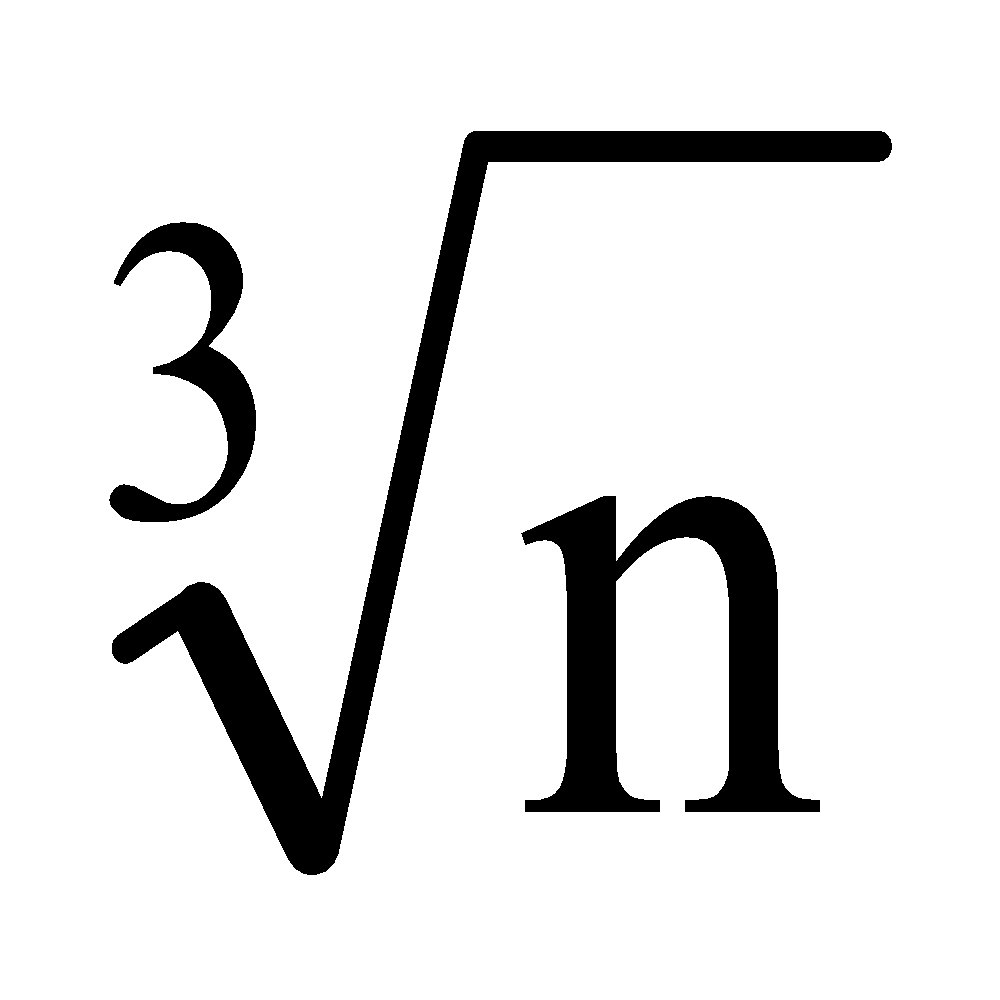 follow the following steps:
follow the following steps:
- Find the prime factorization of ‘n’.
- Group the factors in triples such that all three factors in each triple are the same.
- If some prime factors are left ungrouped, the number ‘n’ is not a perfect cube and the process stops.
- If no factor is left ungrouped, choose one factor form each group and take their product.
- The product is the required cube root of ‘n’.
CUBE ROOT BY HAND:
STEPS:
question 1.  Write down the number of which you wish to calculate the cube root, separating the digits into groups of three, starting at the decimal point, from both directions. Draw a cube radical sign over the number, and put a decimal point over the radical directly above the decimal point in the number. For example, let us calculate
Write down the number of which you wish to calculate the cube root, separating the digits into groups of three, starting at the decimal point, from both directions. Draw a cube radical sign over the number, and put a decimal point over the radical directly above the decimal point in the number. For example, let us calculate
question 2. The cube root of 10, so we separate it as 10. 000 000. 2
question 3. Start with the leftmost group of number(s), and find the biggest integer whose cube is less than or equal to it. Write the integer above the radical, and its cube under the first group. Draw a line under that cube, and subtract it from the first group. In our example, 2^3=8<10<3^3=27, so write 2 over the radical, write 8 under the first group, and subtract it from the first group, resulting in 2.3
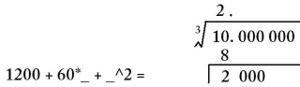
question 4. Bring down the next group of numbers into the remainder, and draw a vertical line to the left of the resulting number. To the left of the vertical line, write three hundred times the square of the number above the radical, a plus sign, thirty times the number above the radical, a multiplication sign, an underscore character, another plus sign, another underscore character, the exponent 2, an equals sign, and some blank space for the answer. For our example, bring down the three 0's. 300 times square of 2 is 1200, 30 times 2 is 60, so write "1200+60*_+_^2=(blank space)" to the left of the vertical line.
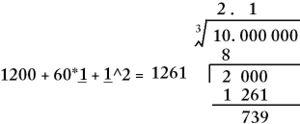
question 5. Find the biggest integer N that would fit into both underscore places, and give a number in the blank space such that integer N times the number is less than the current remainder. Put the integer N above the radical and into both underscore places, calculate the number to the right of the equal sign, multiply this number by N, write the product under the current remainder, draw a line under that, and subtract to obtain the new remainder. For our example, the integer is 1, 1200+60*1+12=1261, and 1*1261=1261, which subtracted from 2000 is 739. If the current answer above the radical has the desired accuracy, stop. Otherwise, proceed to the next step.
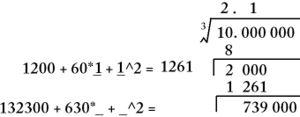
question 6. Repeat the previous two steps to find the next digit in the cube root.
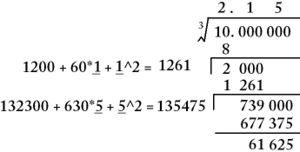
The result above the radical is the cube root, accurate to three significant figures. In our example, the cube root of 10 is 2.15. Verify that by calculating 2.15^3=9.94, which approximates 10. If you need greater accuracy, simply continue the process.
CBSE NCERT Solutions for Class 8 Maths
class 8 maths NCERT solutions Chapter 1: Rational Numbers
class 8 maths NCERT solutions Chapter 2: Linear Equations in One Variable
class 8 maths NCERT solutions Chapter 3: Understanding Quadrilaterals
class 8 maths NCERT solutions Chapter 4: Practical Geometry
class 8 maths NCERT solutions Chapter 5: Data Handling
class 8 maths NCERT solutions Chapter 6: Square and Square Roots
class 8 maths NCERT solutions Chapter 7: Cube and Cube Roots
class 8 maths NCERT solutions Chapter 8: Comparing Quantities
NCERT Class 8 Maths solution Chapter 9: Algebraic Expressions and Identities
class 8 maths NCERT solutions Chapter 10: Visualizing Solid Shapes
class 8 maths NCERT solutions Chapter 11: Mensuration
class 8 maths NCERT solutions Chapter 12: Exponents and Powers
class 8 maths NCERT solutions Chapter 13: Direct and Inverse Proportions
class 8 maths NCERT solutions Chapter 14: Factorization
class 8 maths NCERT solutions Chapter 15: Introduction to Graphs
class 8 maths NCERT solutions Chapter 16: Playing with Numbers
Notes,worksheet and solved question for Maths class 8
- class 8 maths notes on chapter Liner equation in one variable
- class 8 maths notes on chapter algebric expression
- class 8 maths notes on chapter Mensuration
- class 8 maths notes on chapter Square and square roots
- class 8 maths notes on chapter statistice
- class 8 maths notes on chapter practical Geometry
- class 8 maths notes on chapter commericial maths
- class 8 maths notes on chapter solid shape
- class 8 maths notes on chapter quadrilaterals
- class 8 maths notes on chapter exponents
- class 8 maths notes on chapter factorisation
- class 8 maths notes on chapter inverse proporation
- class 8 maths notes on chapter cube and cube roots
Check your marks in a chapter which you have complited in school from Physics Wallah chapter wise online test just click on the link given below









