Fluid Subjected to Constant Acceleration

Fluid Subjected to Constant Acceleration

A fluid, contained in a vessel, may be subjected to a constant linear acceleration without any relative movement being created between different element of the fluid in the vessel. The fluid orient itself to attain a new equilibrium position under the action of the acceleration. Although the fluid is undergoing an acceleration, it is moving with the appearance of a rigid body. The fluid is thus said to be in a state of relative rest. In the absence of relative motion between different fluid elements, the law of fluid statics is applicable.

Consider a liquid contained in a vessel. While at rest, the free surface maintains a horizontal level but in the state of relative rest under a constant acceleration a, the liquid orients itself to maintain the free surface inclined at an angle θ with the horizontal as shown in the fig.(12.25 b). The inclination θ may be related to the magnitude and direction of the acceleration vector by considering the dynamics of an element of the liquid.

Consider a small element of size Δx and Δy at the position coordinates (x, y) as shown in the figure(12.25 b). From the free body diagram we can write the equation of dynamics

along the x -axis  

p(Δy) - 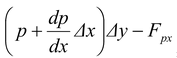= 0

Since Fpx = ρax(Δx)(Δy), therefore,

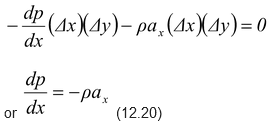
along the y – axis

p(Δx) - 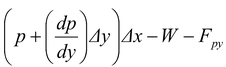= 0

Since W = ρg(Δx)(Δy), and therefore Fpy = ρay(Δx)(Δy)

or 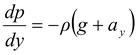(12.21)

Note that if ax= 0 and ay = 0, then

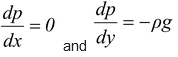
That is, pressure does not vary along the x – axis if ax = 0, thus pressure at all the points on a plane are same when ax ≠ 0 pressure increases in the opposite direction of acceleration.

The angle of inclination of the free surface is obtained by

tanθ = (12.22)