Pressure Measuring Devices
Share
Pressure Measuring Devices
Solids And Fluids of Class 11
Pressure Measuring Devices
A manometer is a tube open at both the ends and bent into the shape of a “U” and partially filled with mercury. When one end of the tube is subjected to an unknown pressure p, the mercury level drops on that side of the tube and rises on the other so that the difference in mercury level is h as shown in the figure.
|
According to Pacal’s Law, when we move down in a fluid pressure increases with depth and when we move up the pressure decreases with depth. When we move horizontally in a fluid pressure remains constant. Therefore, p + ρogho - ρmgh = po where po the atmospheric pressure, and ρo is the density of the fluid inside the vessel |
|
Example: 12.10
|
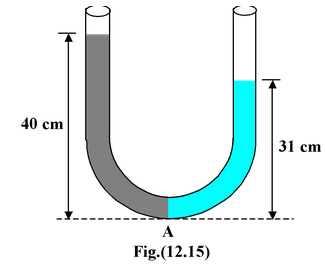
As shown in the figure(12.15), a column of water 40 cm high supports a 31 cm of an unknown fluid. What is the density of the unknown fluid? Solution The pressure at point A due to the two fluids must be equal (or the one with the higher pressure would push the lower pressure fluid away). Therefore, Pressure due to water = pressure due to known fluid |
|
h1ρ1g = h2ρ2 g
from which ρ2 =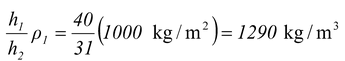 
Example: 12.11
|
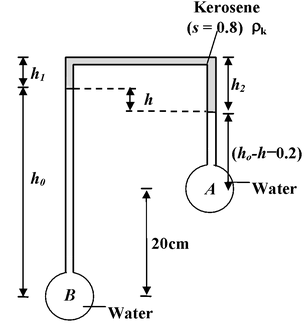
For the arrangement shown in the figure(12.16), determine h if the pressure difference between the vessels A and B is 3 kN/m2. |
|
||
|
Solution Let pressure in the horizontal tube is P So in left vertical tube P + ρkgh1 + ρwgho = PB P + ρkgh2 + ρwg(ho – h – 0.2) = PA here, pB - pA = 3 × 103 N/m2, ρw = 103 kg/m3 ρk = 800 kg/m3. Thus,h = 0.5 m = 50 cm |
|
||
The Mercury Barometer
|
It is a straight glass tube (closed at one end) completely filled with mercury and inserted into a dish which is also filled with mercury as shown in the figure(12.17). Atmospheric pressure supports the column of mercury in the tube to a height h. The pressure between the closed end of the tube and the column of mercury is zero, p = 0. |
|
Therefore, pressure at points A and B are equal and thus
po = 0 + ρmgh
At the sea level, po can support a column of mercury about 76 cm in height.
Hencepo = (13.6 × 103)(9.81)(0.76) = 1.01 × 105 Nm-2 (or Pa)
Example: 12.12
What must be the length of a barometer tube used to measure atmospheric pressure if we are to use water instead of mercury.
Solution
We know that
po = ρmghm = ρwghw
whereρw and hw are the density and height of the water column supporting the atmospheric pressure po.
∴hw = 
Since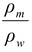
= 13.6 and hm = 0.76 m
∴hw = (13.6)(0.76) = 10.33 m
|
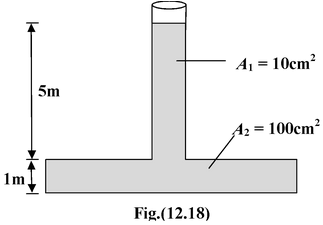
Example: 12.13 In the figure shown , find (a)the total force on the bottom of the tank due to the water pressure. (b)the total weight of water . Why is there a difference between the two ? |
|
Solution
(a)Pressure at the base due to water is
p = ρwg [ 5 + 1] = (103)(10)(5 + 1) = 6 × 104 N/m2
∴Force = pA2 = (6 × 104)(100 × 10-4) = 600 N
(b)Weight of water = ρw g [5A1 + A2] = 104 [5 × 10 × 10-4 + 100 × 10-4] = 150 N
