Density and Pressure
Share
Density and Pressure
Solids And Fluids of Class 11
Density and Pressure
The density ρ of a substance is defined as the mass per unit volume of a sample of the substance.
If a small mass element Δm occupies a volume ΔV, the density is given by
ρ = Δm/ΔV
In general, the density of an object depends on position, so that
ρ = f(x, y, z)
If the object is homogeneous, its physical parameters do not change with position throughout its volume. Thus, for a homogeneous object of mass M and volume V, the density is defined as
ρ = M/V (12.11)
The SI units of density are kg m-3.
Specific Gravity
The specific gravity of a substance is the ratio of its density to that of water at 4oC, which is 1000 kg/m3. Specific gravity is a dimensionless quantity numerically equal to the density quoted in g/cm3. For example, the specific gravity of mercury is 13.6, and the specific gravity of water at 100oC is 0.998.
Example: 12.4
Find the density and specific gravity of gasoline if 51 g occupies 75 cm3?
Solution
Density = mass/volume =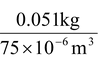 
= 680 kg/m3
Sp.gr =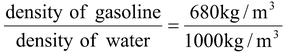 
= 0.68
orSp. gravity = 
Example: 12.5
The mass of a liter of milk is 1.032 kg. The butterfat that it contains has a density of
865 kg/m3 when pure, and it constitutes 4 percent of the milk by volume. What is the density of the fat-free skimmed milk?
Solution
Volume of fat in 1000 cm3 of milk = 4% × 1000 cm3 = 40 cm3
Mass of 40cm3 fat = vρ = (40 × 10-6 m3)(865 kg/m3) = 0.0346 kg
Density of skimmed milk = mass/volume =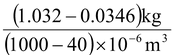 
= 1039 kg/m3
Pressure
|
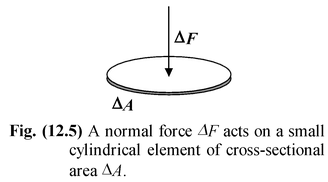
The pressure exerted by a fluid is defined as the force per unit area at a point within the fluid. Consider an element of area ΔA as shown in figure on which an external force ΔF is acting normal to the surface. The average pressure in the fluid at the position of the element is given by pav = ΔF/ΔA |
|
As ΔA → 0, the element reduces to a point, and thus, pressure at a point is defined as
p =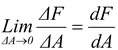 
(12.12)
When the force is constant over the surface A, the above equation reduces to
p = F/A (12.13)
The SI unit of pressure Nm-2 and is also called pascal (Pa).
The other common pressure unit are the atmosphere and bar.
1 atm = 1.01325 × 105 Pa
1 bar = 1.00000 × 105 Pa
Example: 12.6
Atmospheric pressure is about 1.01 × 105 Pa. How large a force does the atmosphere exert on a 2 cm2 area on the top of your head?
Solution
Because p = F/A, where F is perpendicular to A, we have F = pA. Assuming that 2 cm2 of your head is flat (nearly correct) and that the force due to the atmosphere is perpendicular to the surface (as it is), we have
F = pA = (1.01 × 105 N/m2)(2 × 10-4m2) ≈ 20 N
Pressure is Isotropic
|
Imagine a static fluid and consider a small cubic element of it deep within the fluid as shown in figure(12.6). Since this fluid element is in equilibrium, therefore, forces acting on each lateral face of this element must also be equal in magnitude. Because the areas of each face are equal, therefore, the pressure on each of the lateral faces must also be the same. In the limit as the cube element reduces to a point, the forces on the top and bottom surfaces also become equal. Thus, the pressure exerted by a fluid at a point is the same in all directions –– the pressure is isotropic. |
|
Since the fluid cannot support a shear stress, the force exerted by a fluid pressure must also be perpendicular to the surface of the container that holds it.
