OPERATIONS OF ALGEBRAIC EXPRESSIONS

Algebraic expressions of Class 8

(1) The plus sign (+) indicates what number is to be added to what precedes it

e.g. : p + q

(2) The minus sign (–) when placed before a number indicates that the number is to be subtracted from what precedes it

e.g.: x – y

(3) The sign plus or minus (+) is read plus or minus and when placed before a number. indicates that the number is to be either added to or subtracted from what precedes it.

(4) The sign ~ when placed between the two numbers indicates that the less of the two is to be subtracted from the greater

e.g. If a = 5, b = 8, then a ~ b mean 8 – 5 = 3

(5) An intelligible collection of letters and signs of operation is called an algebraic expression. The parts of an algebraic expression that are connected by the + or – are called its terms.

E.g.: 7a + ab + c × d – 2c × f g is an algebraic expression

7a, ab + c × d, – 2c × f g are called terms

(6) Expressions are either simple or compound.

WORKING RULES FOR ADDITION OF ALGEBRAIC EXPRESSIONS:

Rule 1: When 2 positive quantities are added the sum is a positive quantity

(+a) + (+b) = + (a + b)

e.g.: (+7a) + (+5a) = + (7a + 5a) = +12a

Rule 2: When 2 negative quantities are added together the sum is a negative quantity.

(–a) + (–b) = – (a + b)

e.g.: (– 8x) + (– 6x) = – (8 + 6)x = – 14x

Rule 3: When a negative quantity is added to a positive quantity, the sign of the result is positive or negative according as the absolute value is less or greater than that of the positive quantity and the absolute value of the result is always equal to the difference between the absolute values of the quantities.

If a > b (– a) + (+ b) = – (a – b) Eg: (– 7a) + (+ 3a) = – 4a

If a < b (– a) + (+ b) = + (b – a) E.g.: (– 2a) + ( + 7a) = + 5a

When any number of quantities are added together the result will be the same in whatever order the quantities may be taken.

E.g.: (– a) + (+ b) = (+b) + (– a), (– 8p) + (+ 3p) = (+ 3p) + (– 8p)

When any number of quantities are added together they can be divided into groups and the result expressed as the sum of the these groups.

– 7y + 6y + 2y – 8y + 9y + 3y = (– 7y + 6y) + (2y – 8y) + (9y + 3y)

= (– 1y) + (– 6y) + (12y) = (– 7y) + (12y) = + 5y

When any number of quantities are to be added some of which are positive and other negative, then collect the positive terms in one group and the negative terms in another and express the result as the sum of there groups.

4m – 3m + 2m – 9m + 8m – 6m = (4m + 2m + 8m) – (+3m + 9m + 6m)

= (+ 14m) – (+ 18m) = – 4m

Column method for addition of Algebraic expressions:

Write each expression in a separate row such that their like terms are arranged one below the other in a column. Then the terms are added column wise.

Add 7a2 + 3a – 8 and – 2a2 + 4a – 3

7a2 + 3a – 8

– 2a2 + 4a – 3

_____________

+ 5a2 + 7a – 11

Horizontal method for addition of algebraic expressions:

We add two or more expressions by collecting the like terms together and then simplifying.

E.g.: 7x + 3y – 2z is added to – 2x + 4y + 3z

= 7x – 2x + 3y + 4y – 2z + 3z

= 7x + (– 2x) + (+3y) + (+4y) +(– 2z) + (+3z) = 5x + 7y + 1z

E.g. is added to =

L.C.M of 2 and 3 is 6. L.C.M of 3 and 6 is 6

WORKING RULE FOR SUBTRACTION OF ALGEBRAIC EXPRESSION:

Any quantity b is said to be subtracted from any other quantities a, when a third quantity c is found such that the sum of b and c is equal to a. In other words c = a – b. When c is such that a = b + c, a is called minuend, b is called subtrahend and c is called the remainder.
Subtraction of like terms can be performed in a manner exactly similarly to that used in subtraction of integers. For any 2 integers a and b we have a – b = a + (additive inverse of b). Change the sign of term to be subtracted and add the new monomial to the one from which subtraction is to be made.

E.g.: (+7a) – (+ 3a) = + 7a + (– 3a) = + 4a

(– 8a) – (– 2a) = (– 8a) + (+ 2a) = – 6a

(– 5a) – (+ 3a) = (– 5a) + (– 3a) = – 8a

(+ 8a) – (– 2a) = (+ 8a) + (+ 2a) = + 10a

(– 6a) – (– 9a) = (– 6a) + (+ 9a) = + 3a

Column method for subtraction of Algebraic expressions:

question Write the expression to be subtracted below the other expression such that like terms of the two expressions are in the same column. Now change the sign of each term of lower expression and add term wise

e.g. subtract 3p – 8q + 5r from 7q + 10p – 3r

7q + 10p – 3r

– 8q + 3p + 5r

+ – –

_____________

15q + 7p – 8r

Horizontal method for subtraction of Algebraic expressions:

Change the sign of each term of the expression to be subtracted and then add

E.g.: 7a3 + 3a2 – 8a + 6) – (3a3 – 2a2 + 3a – 7)

= (7a3 +3a2 – 8a + 6) + (– 3a3 + 2a2 – 3a + 7)

= (7a3) + (– 3a3) + (3a2) + (2a)2 + (– 8a) + (– 3a) + (+ 6) + (+ 7) = 4a3 + 5a2 – 11a + 13

E.g.: =

question What should be added to 2x – 3y + 5z to get 7x – 3y + 2z

7x – 3y + 2z

2x – 3y + 5z

– + –

__________

5x – 3z should be added

question What should be subtracted from 2x2 – 9x + 6 to get 3x2 –2x + 7

2x2 – 9x + 6

3x2 – 2x + 7

– + –

______________

– x2 – 7x – 1 should be subtracted from 2x2 – 9x + 6

question By how much 7x – 3y + 2z exceeds 2x + 7y – 8z

7x – 3y + 2z

2x + 7y – 8z

– – +

_______________

5x – 10y + 10z

question From the sum of 2x + 3y – 5z, 4x – 2y + 7z, subtract 5x – 9y – 2z

2x + 3y – 5z

+ 4x – 2y + 7z

________________

6x + y + 2z

+ 5x – 9y – 2z

– + +

______________

x + 10y + 4z

question Multiplication of Monomials

Product of monomials = (Product of their numerical coefficients) (Product of their variable parts)

The product law of exponents i.e. 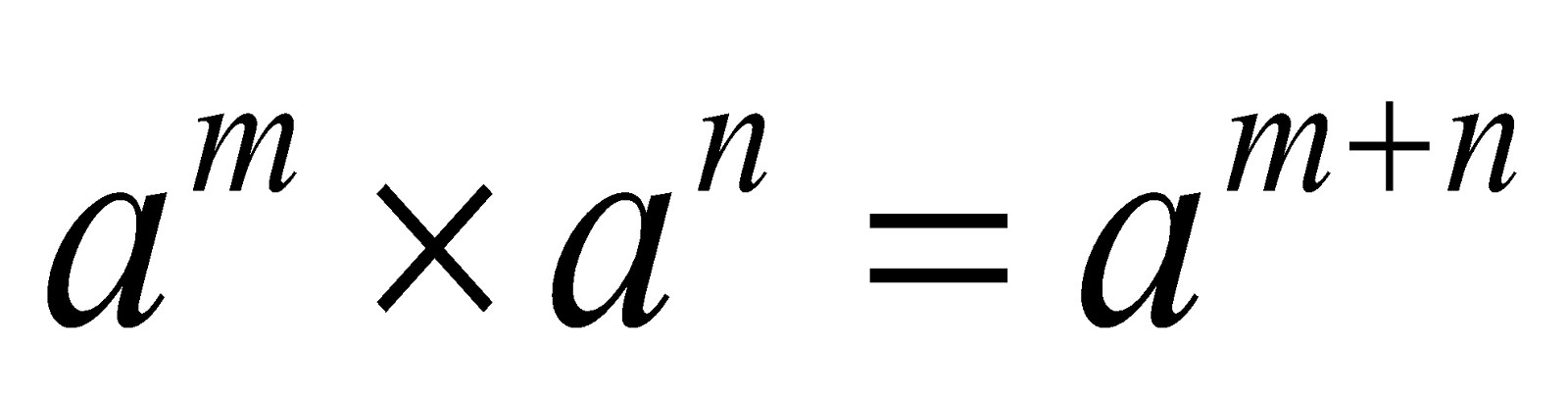finds great use in the multiplication of algebraic expressions.

MULTIPLICATION OF ALGEBRAIC EXPRESSIONS:

Working Rule

question 1. The number multiplied is called the multiplicand (28xy) and the number by which it is multiplied is called the multiplier; (4) the result is called the product (112xy)

e.g.: 28xy × 4 = 112xy

question 3. The law of signs

(+ a) × (+ b) = + ab

(– a) × (– b) = + ab

(+ a) × (– b) = – ab

(– a) × (+ b) = – ab

question4. Laws of multiplication