WORD PROBLEMS INVOLVING INVERSE PROPORTIONS

Inverse proportionality is exactly opposite to directly proportions i.e. two variables are said to be inversely proportional if an increase in value of one variable results in a decrease in value of the other variable and similarly a decrease in value of one variable results in an increase in value of the other variable. The questions are also of the form, "If x results in a, what will be the result if  x changes to y?

You need a simple 4 step approach to solve the problems:

• Identify Variables: Usually this is a simpler thing to do. The variables are fairly obvious in typical proportion problems.
• Understand the Relationship: Is the relationship between variables inversely proportional? Understand the context and use common sense. For example the following relationships are inversely proportional
• The time a car needs to travel between two towns is inversely proportional to its speed i.e. higher the speed the less time it takes to cover the same distance
• The time it takes to do a job is inversely proportional to the number of people employed to do the job i.e. if it takes 4 men to complete a wall in 2 days, 8 men can do the same job in 1 day.
• Express the proportionality: Get the problem to a form: "If x results in a, what will be the result if  x changes to y?"

question 1. A car takes 1 hour and 30 minutes to travel the distance between two cities during rush hour. If the average speed is 50% more during off-peak hours, what time will it take to cover the same distance between the two cities during off peak hours (1 hour = 60 minutes)?

(a) 45 Minutes (b) 1 Hour (c) 1 Hour 15 Minutes

(d) 90 Minutes (e) 1 Hour 45 minutes

Solution: Step 1: The time taken to cover the distance and the speed are inversely proportional. Let the speed during rush hour be 8. 

The average speed is 50% more during off-peak hours therefore off-peak hour speed = 1.5s

Step 2: With speed s it takes 1 hour 30 minutes = 1 × 60 + 30 = 90 minutes

Since the speed and time are inversely proportional, the time taken with speed 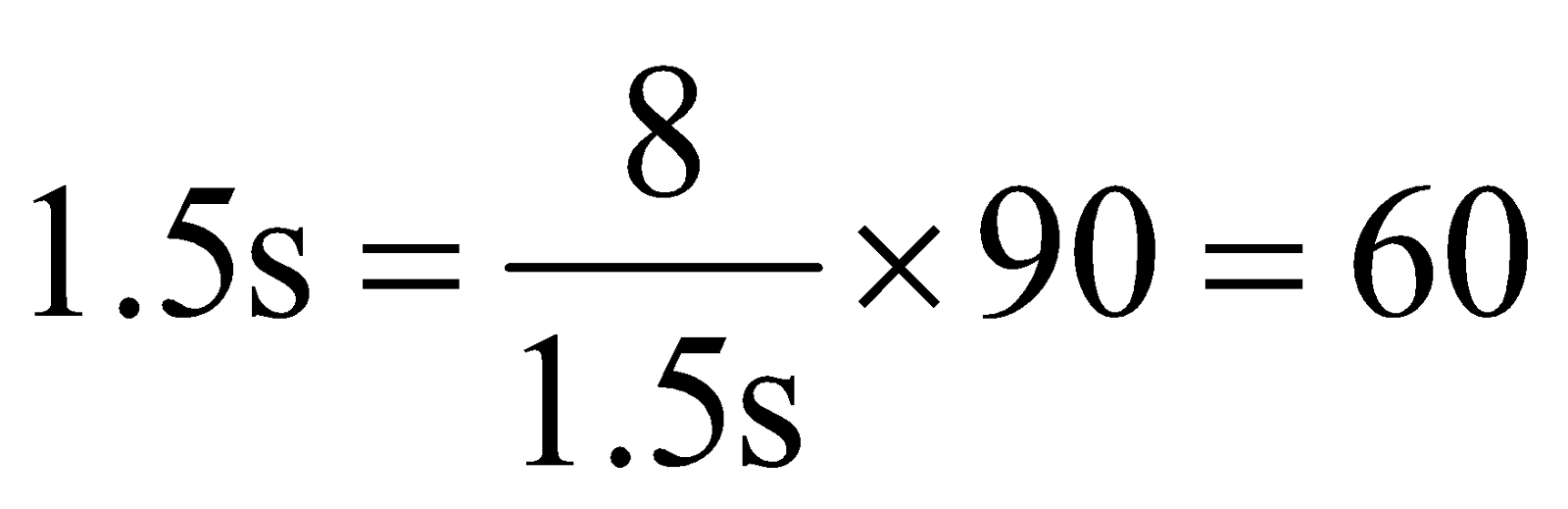 Minutes or 1 Hour

The correct answer is B

CBSE NCERT Solutions for Class 8 Maths

class 8 maths NCERT solutions Chapter 1: Rational Numbers

class 8 maths NCERT solutions  Chapter 2: Linear Equations in One Variable

class 8 maths NCERT solutions  Chapter 3: Understanding Quadrilaterals

class 8 maths NCERT solutions Chapter 4: Practical Geometry

class 8 maths NCERT solutions  Chapter 5: Data Handling

class 8 maths NCERT solutions  Chapter 6: Square and Square Roots

class 8 maths NCERT solutions  Chapter 7: Cube and Cube Roots

class 8 maths NCERT solutions  Chapter 8: Comparing Quantities

NCERT Class 8 Maths solution Chapter 9: Algebraic Expressions and Identities

class 8 maths NCERT solutions  Chapter 10: Visualizing Solid Shapes

class 8 maths NCERT solutions Chapter 11: Mensuration

class 8 maths NCERT solutions  Chapter 12: Exponents and Powers

class 8 maths NCERT solutions  Chapter 13: Direct and Inverse Proportions

class 8 maths NCERT solutions  Chapter 14: Factorization

class 8 maths NCERT solutions  Chapter 15: Introduction to Graphs

class 8 maths NCERT solutions  Chapter 16: Playing with Numbers

Notes,worksheet and solved question for Maths class 8 

1.  class 8 maths notes on chapter Liner equation in one variable
2. class 8 maths notes on chapter algebric expression 
3. class 8 maths notes on chapter Mensuration 
4. class 8 maths notes on chapter Square and square roots 
5. class 8 maths notes on chapter statistice
6. class 8 maths notes on chapter practical Geometry
7. class 8 maths notes on chapter commericial maths
8. class 8 maths notes on chapter solid shape
9. class 8 maths notes on chapter quadrilaterals
10. class 8 maths notes on chapter exponents
11. class 8 maths notes on chapter factorisation 
12. class 8 maths notes on chapter inverse proporation 
13. class 8 maths notes on chapter cube and cube roots 

Check your marks in a chapter which you have complited in school from Physics Wallah chapter wise online test just click on the link given below

chapter wise online test for class 8 maths