SQUARE OF NATURAL NUMBERS FORMS A PATTERN
Square and square roots of Class 8
ADDING ODD NUMBERS:
The sum of first n odd natural numbers is n2
i.e., 1 + 3 + 5 = 9 = 32
1 + 3 + 5 + 7 = 16 = 42 etc.
- Square as sum of two consecutive integers
32= 9 = 4 + 5
First number = 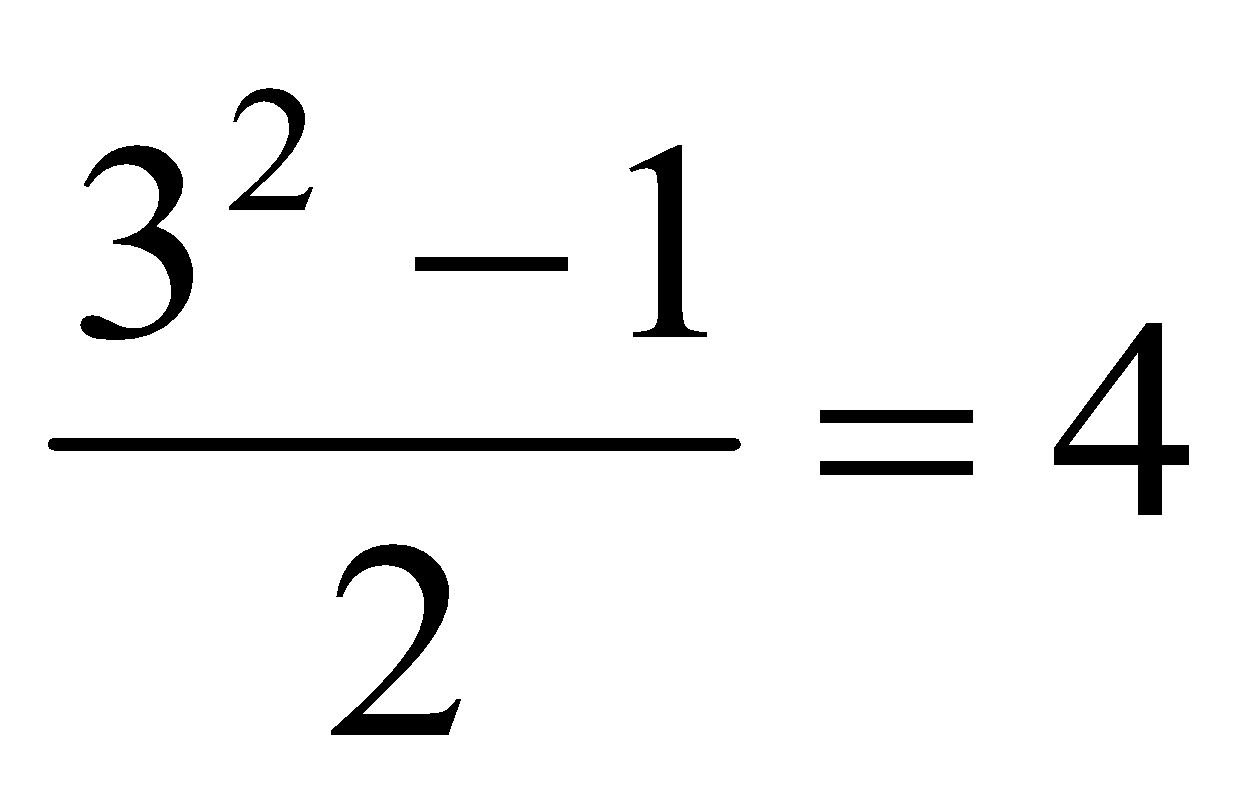
Second number = 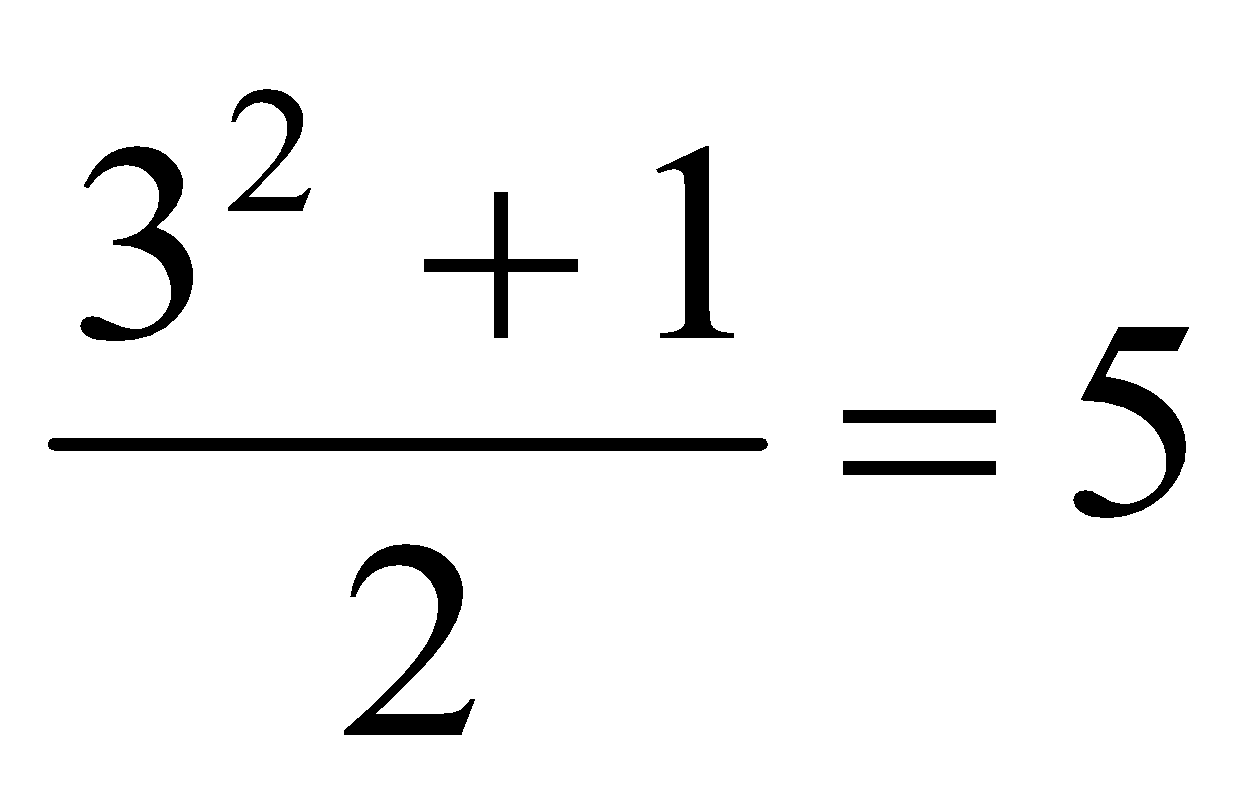
Similarly 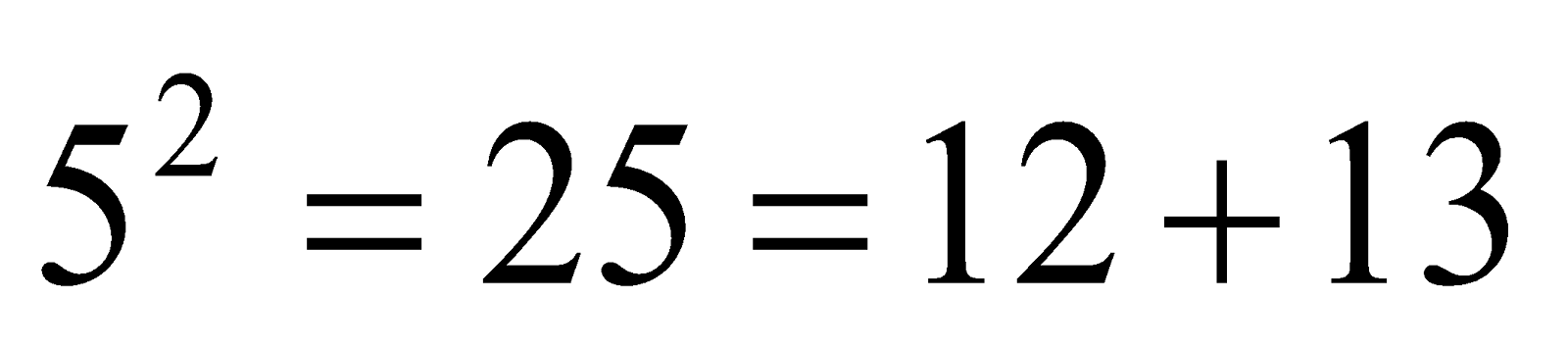

- Product of two consecutive even or odd natural numbers:(a + 1) (a – 1) = (a2 – 1).
- Numbers between squares numbers
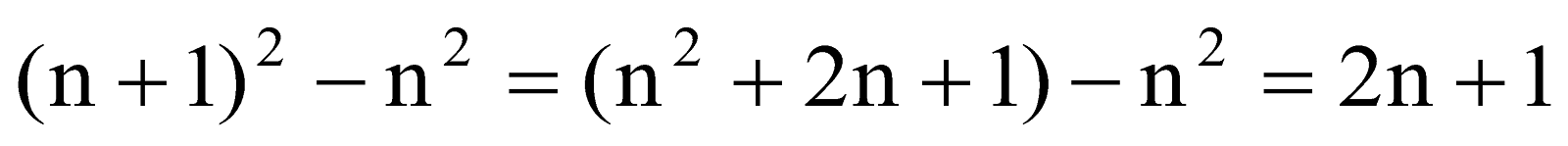
There are 2n non perfect square numbers between the squares of the numbers n and (n + 1).
- Observe the squares of numbers; 1 11, 111 ..... etc. They give an interesting pattern:
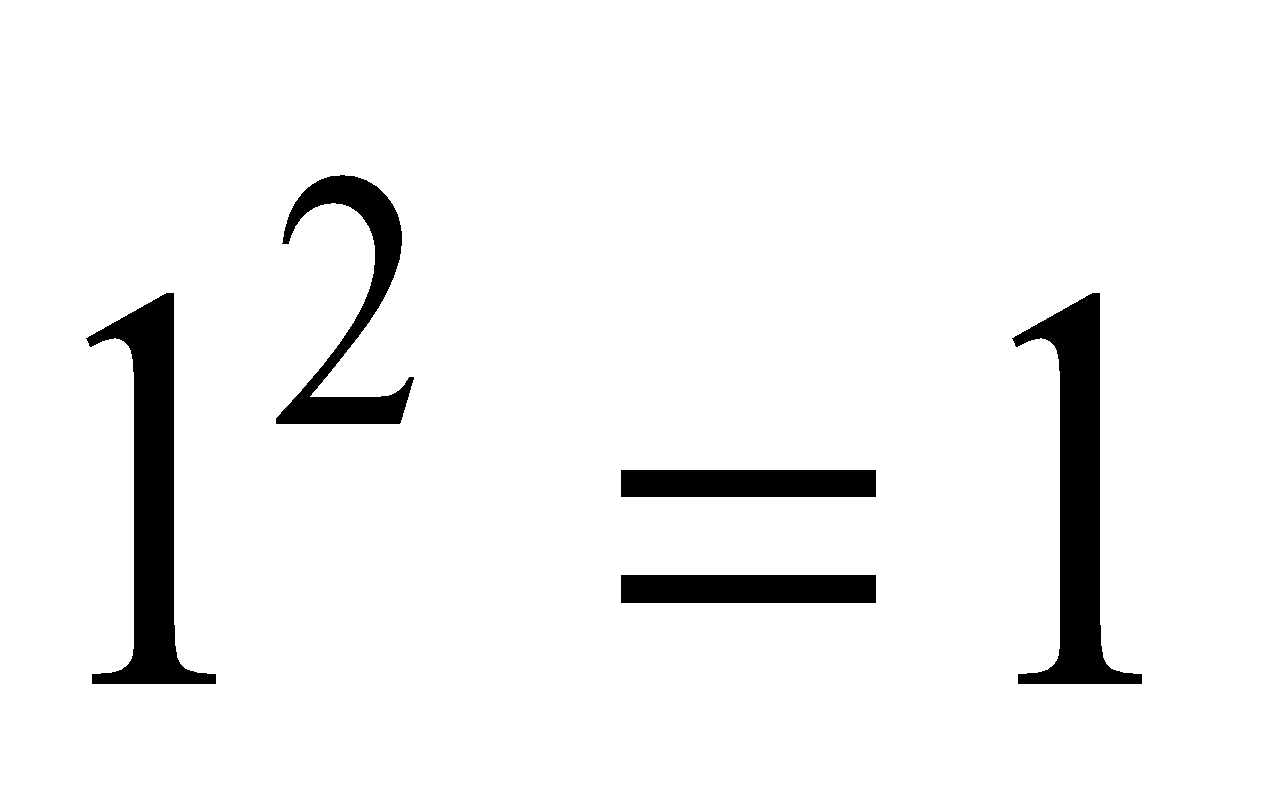
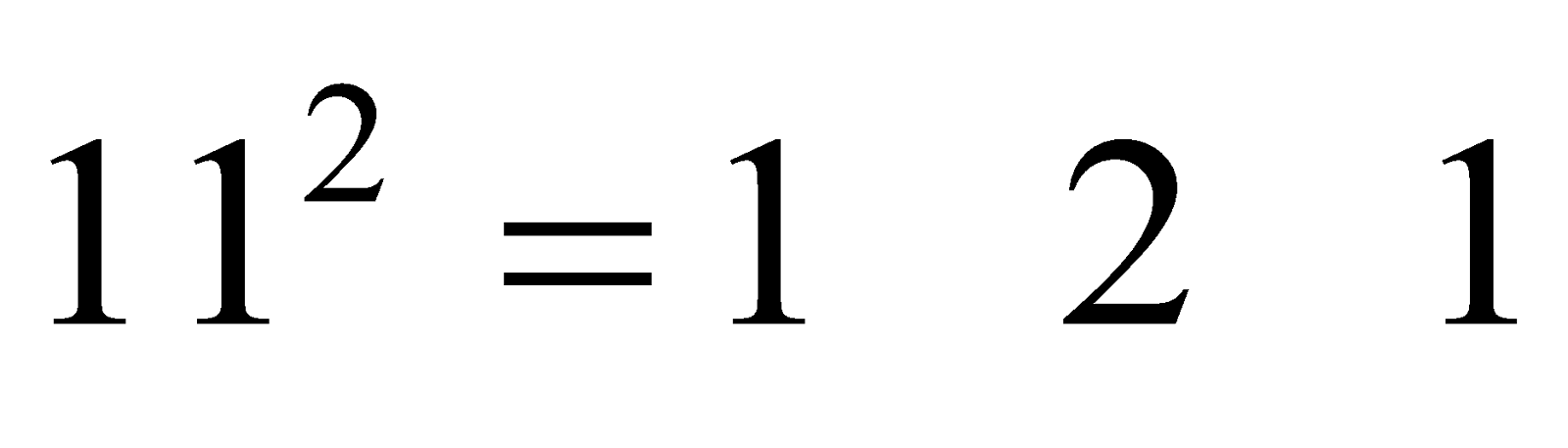
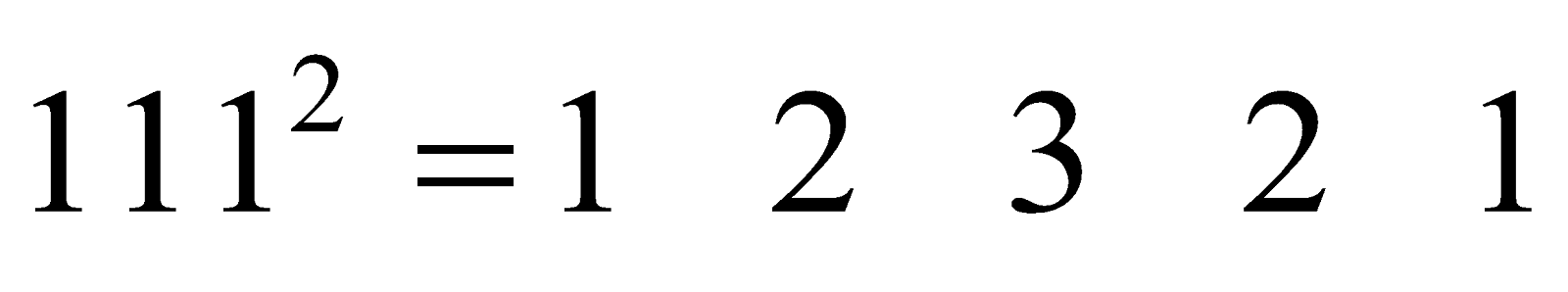
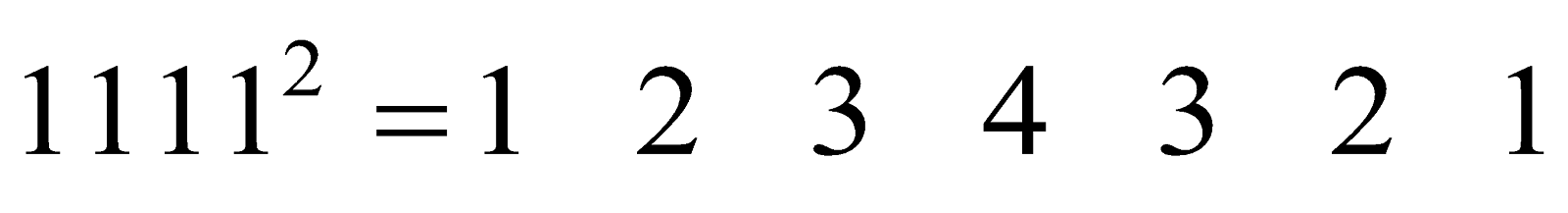
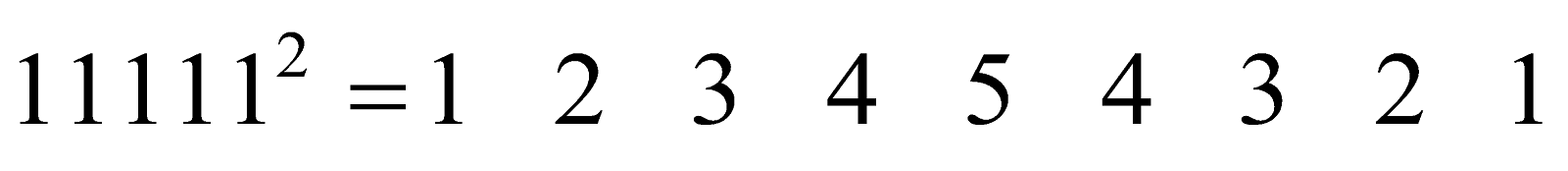
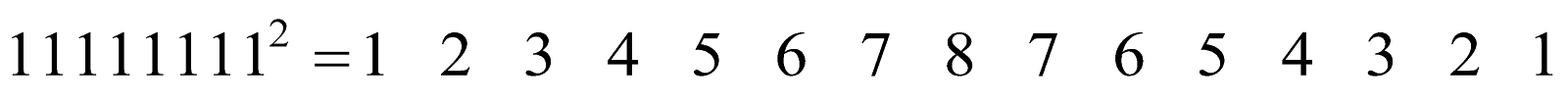
Another interesting pattern

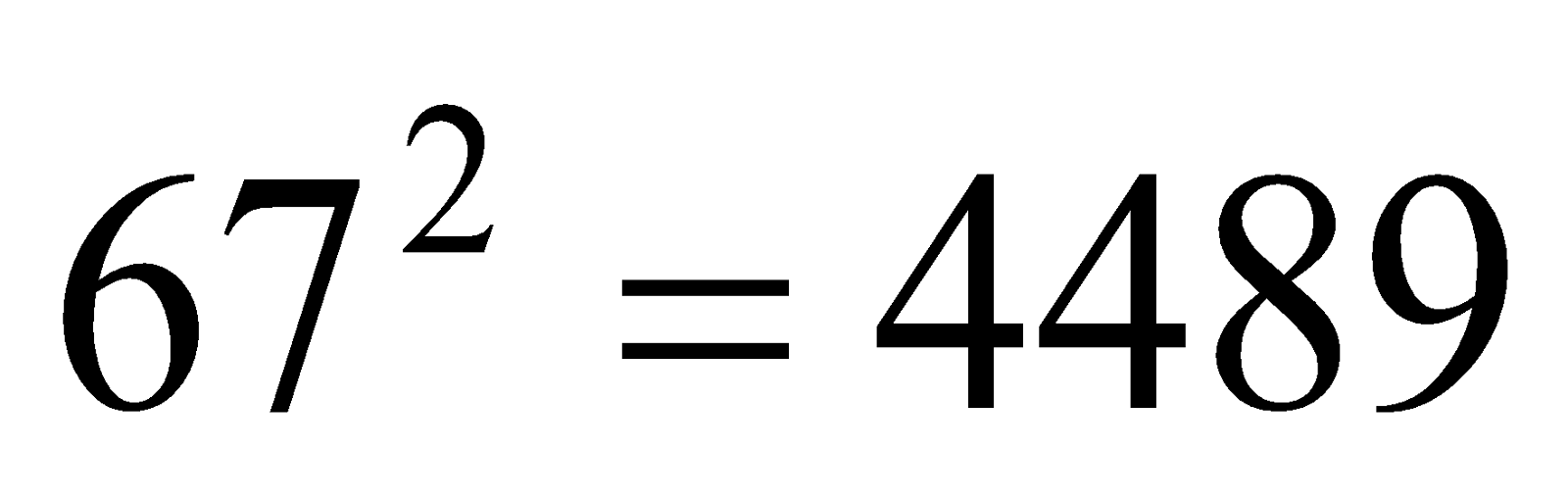

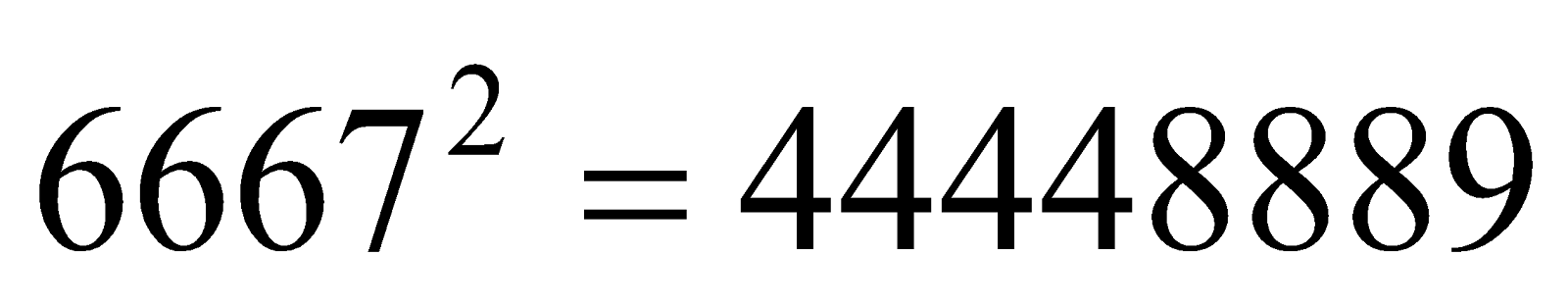
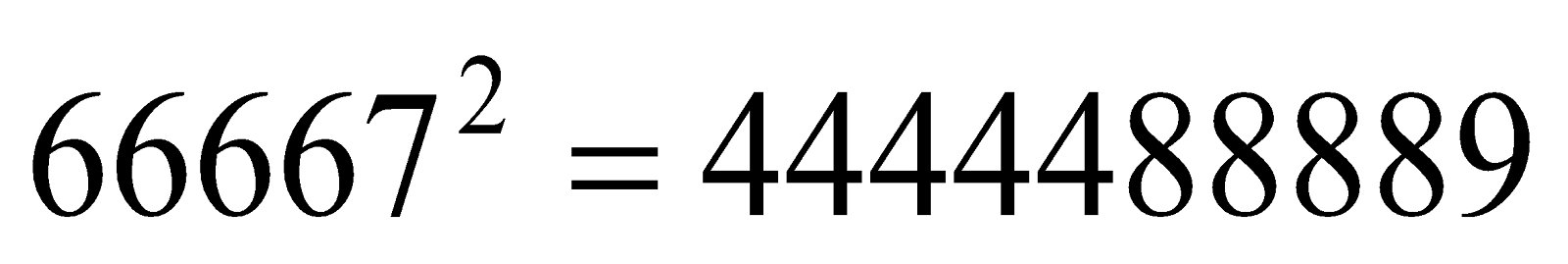

|
|
A natural number is not a perfect square when it cannot be expressed as a sum of successive odd natural numbers starting with 1. |
- If we subtract the consecutive odd natural number starting from 1 and the final result is zero, then the number in a perfect square.
e.g., 16 – 1 = 15
15 – 3 = 12
12 – 5 = 7
7 – 7 = 0
∴ 16 =  (Here, subtraction is 4 times)
(Here, subtraction is 4 times)
- Finding the square of a number
Consider a number with unit digit 5, i.e., a5
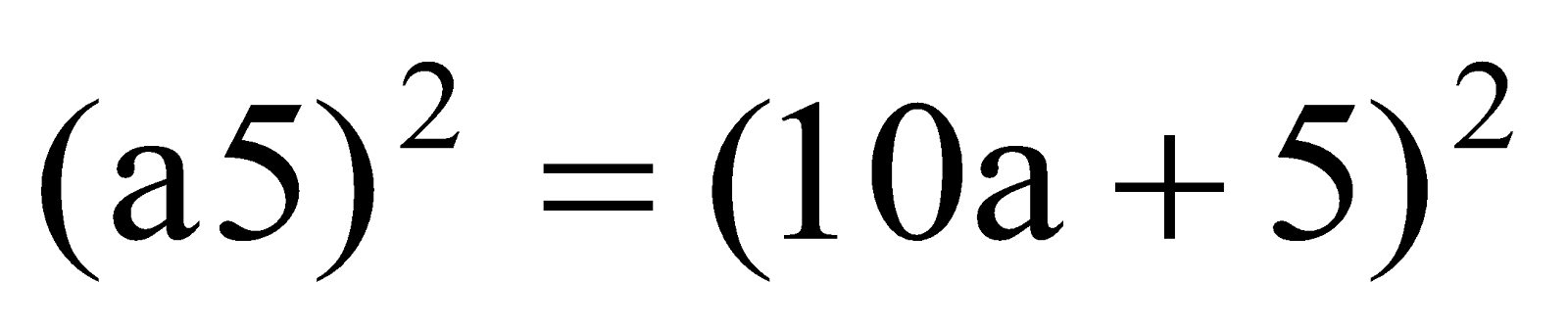
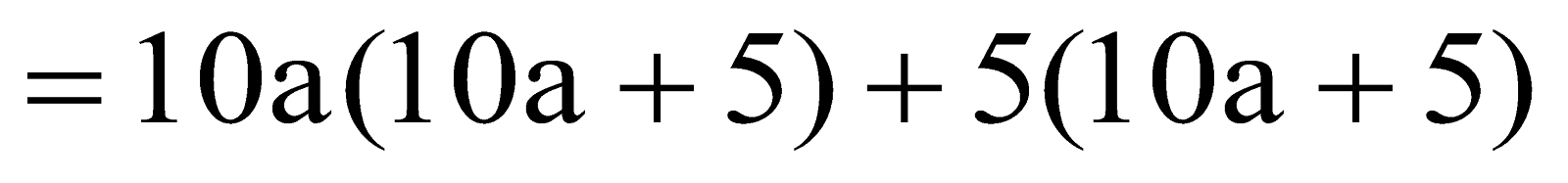
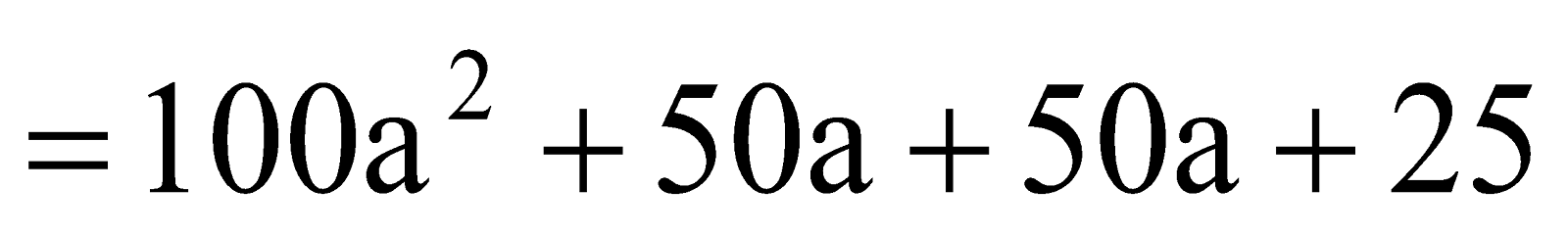
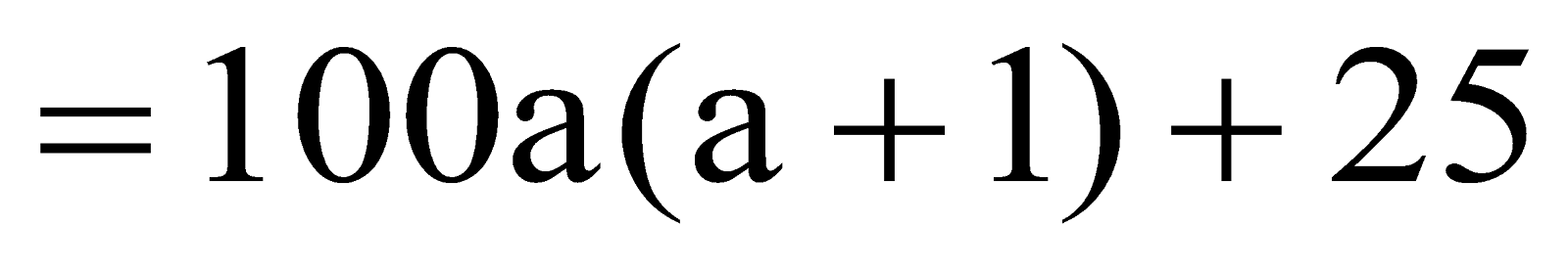
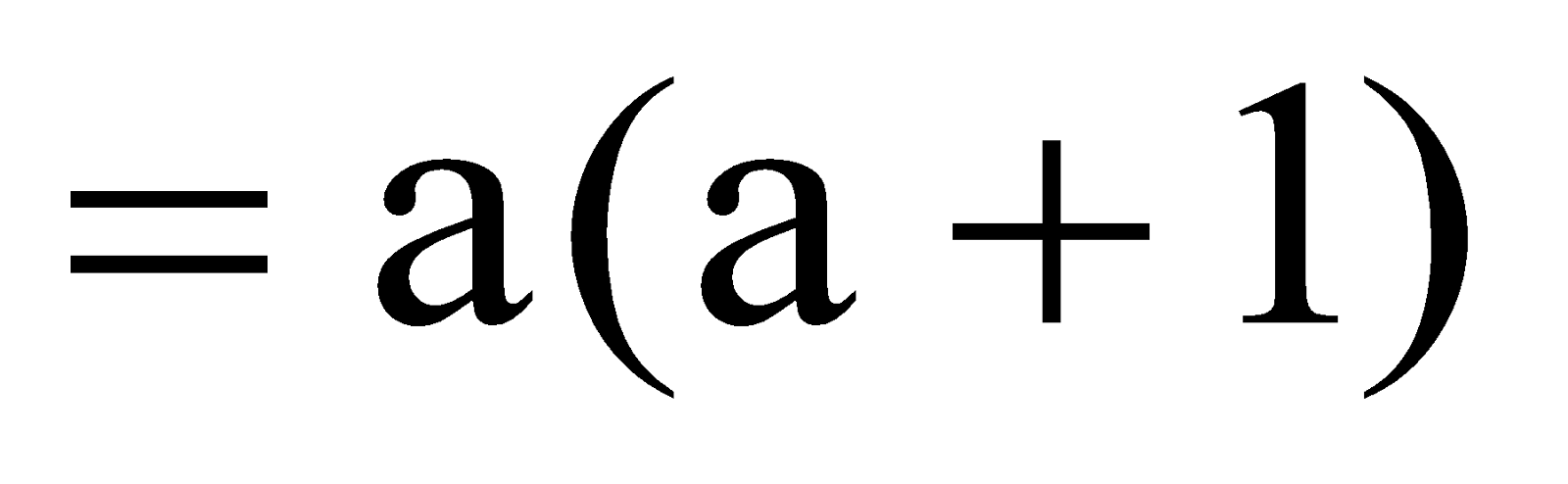 hundred + 25
hundred + 25
-
If a perfect square is of n-digits, then its square root will have
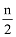 digits if n is even or
digits if n is even or 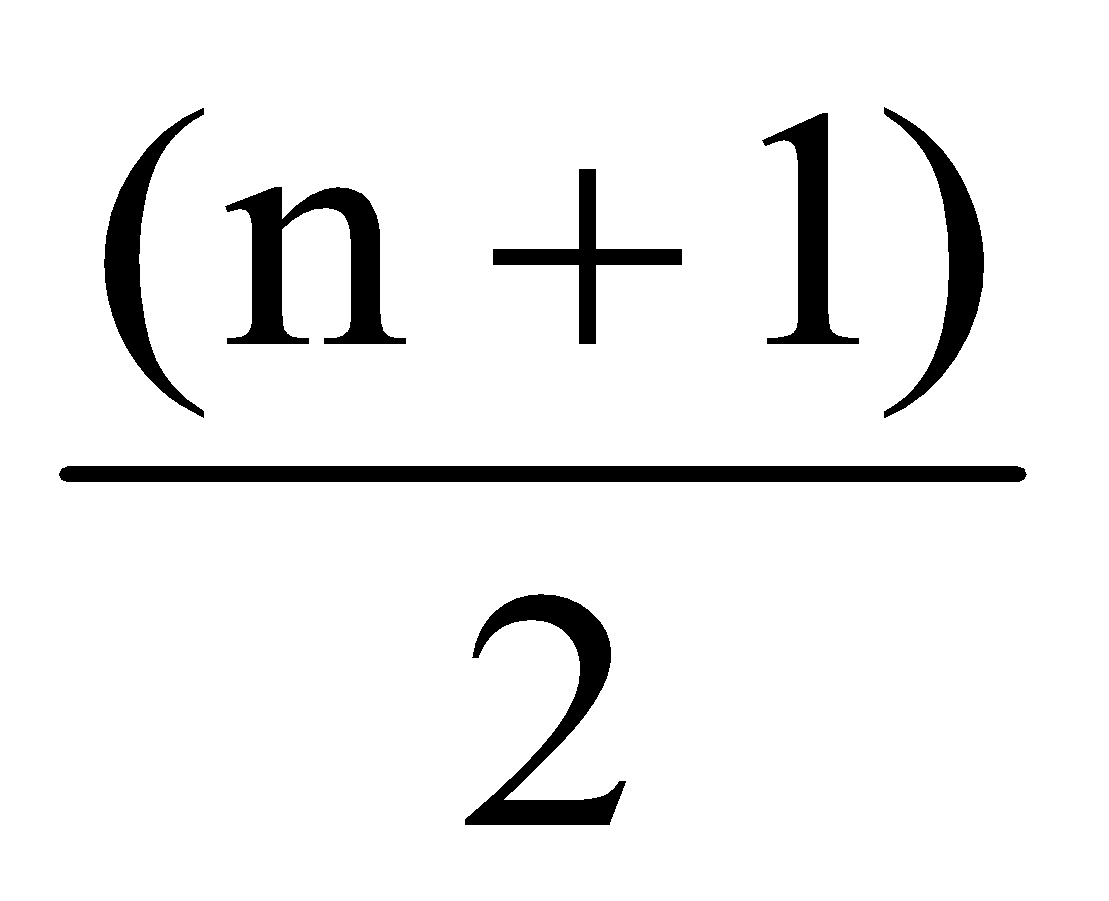 if n is odd.
if n is odd.
PYTHAGOREAN TRIPLETS
"Pythagorean triples" are integer solutions to the Pythagorean Theorem:
For a right triangle, the c side is the hypotenuse, the side opposite the right angle. The a side is the shorter of the two sides adjacent to the right angle. The first rules for determining a subset of Pythagorean triplets are as follows:
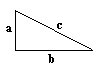
a2 + b2 = c2.
- Every odd number is the a side of a Pythagorean triplet.
- The b side of a Pythagorean triplet is simply (a2 - 1) / 2.
- The c side is b + 1.
Here, a and c are always odd; b is always even. These relationships hold because the difference between successive square numbers is successive odd numbers. Every odd number that is itself a square (and the square of every odd number is an odd number) thus makes for a Pythagorean triplet. Thus, the square of 7, 49, is the difference between 576, the square of 24, and625, the square of 25, giving us the triplet 7,24,25. Similarly, the square of 23, 529, is the difference between 69696, the square of 264, and 70225, the square of 265, giving us the triplet23,264,265.
SQUARE ROOTS:
A number which, when multiplied by itself, results in another number.
e.g. 5 is the square root of 25.
5 = √25
To simplify a square root, you "take out" anything that is a "perfect square"; that is, you take out front anything that has two copies of the same factor:
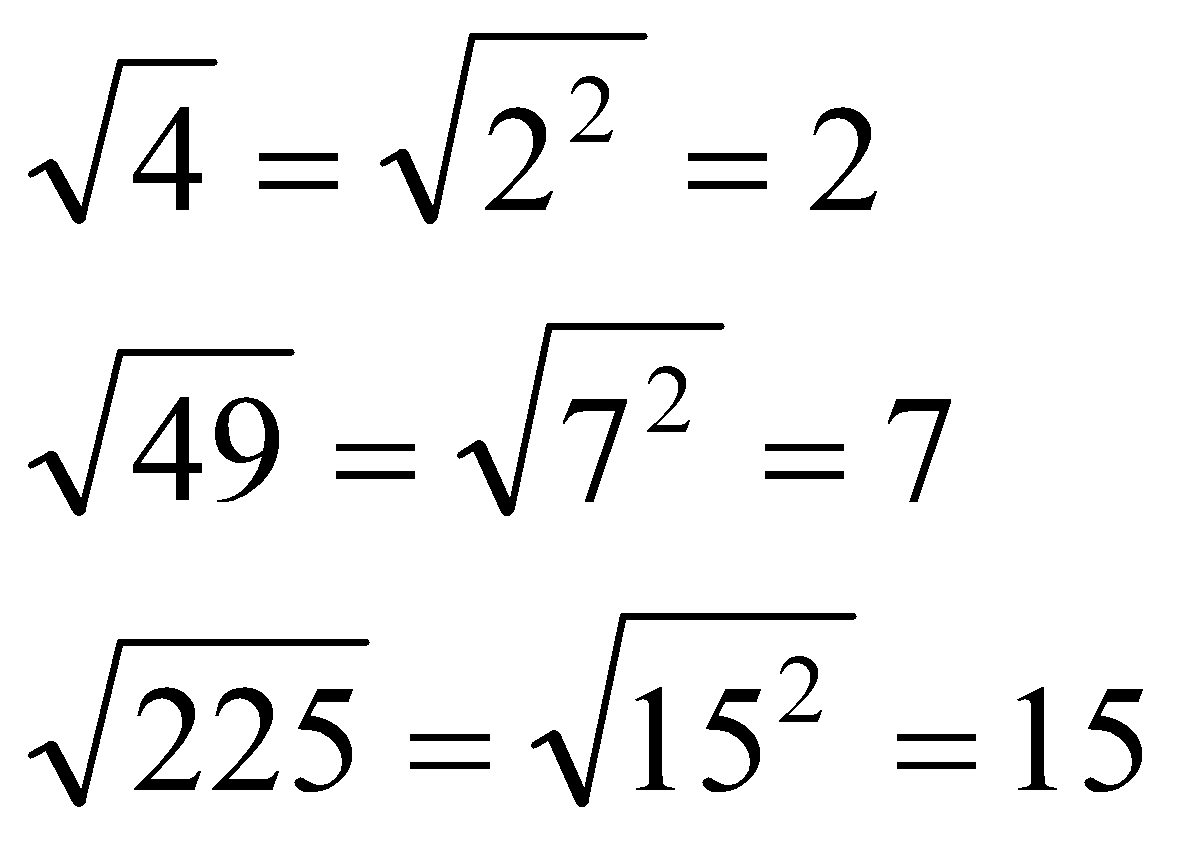
Note that the value of the simplified radical is positive. While either of +2 and –2 might have been squared to get 4, "the square root of four" is defined to be only the positive option, +2. When you solve the equation x2 = 4, you are trying to find all possible values that might have been squared to get 4. But when you are just simplifying the expression 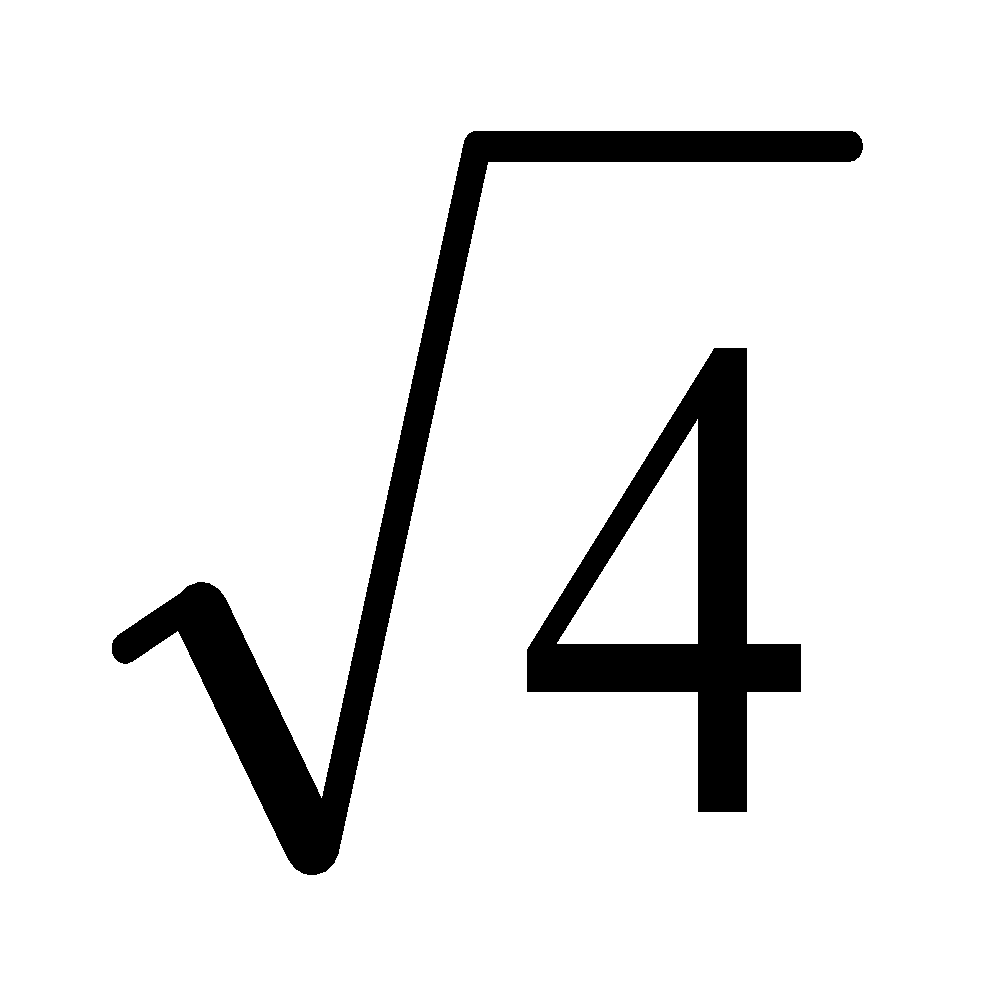 , the ONLY answer is "2"; this positive result is called the "principal" root. (Other roots, such as –2, can be defined using graduate-school topics like "complex analysis" and "branch functions", but you won't need that for years, if ever.)
, the ONLY answer is "2"; this positive result is called the "principal" root. (Other roots, such as –2, can be defined using graduate-school topics like "complex analysis" and "branch functions", but you won't need that for years, if ever.)
Sometimes the argument of a radical is not a perfect square, but it may "contain" a square amongst its factors. To simplify, you need to factor the argument and "take out" anything that is a square; you find anything you've got a pair of inside the radical, and you move it out front. To do this, you use the fact that you can switch between the multiplication of roots and the root of a multiplication. In other words, radicals can be manipulated similarly to powers:
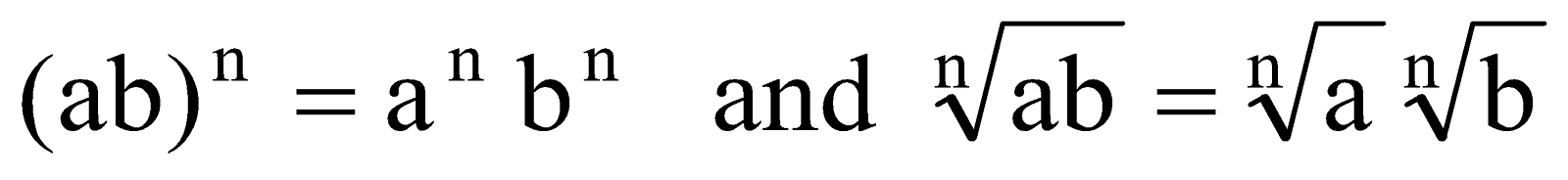
question 1. Simplify 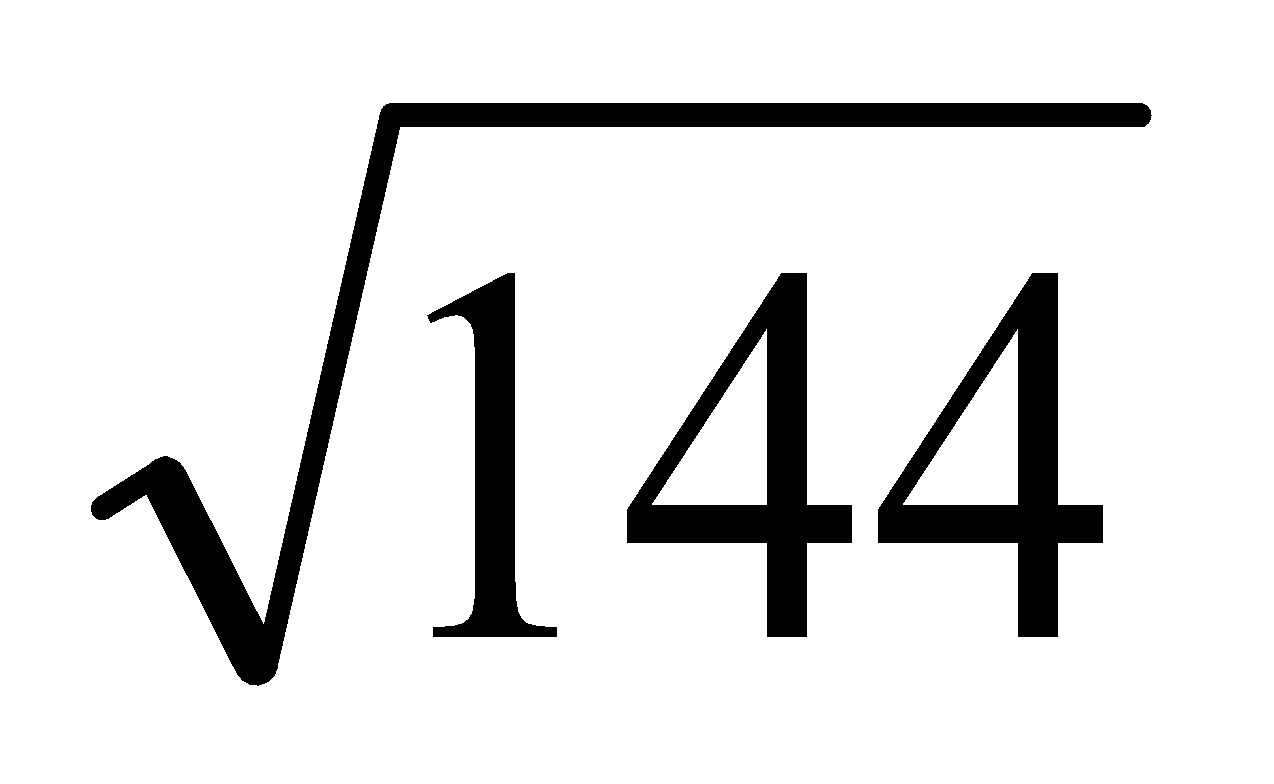
Sol. There are various ways I can approach this simplification. One would be by factoring and then taking two different square roots:
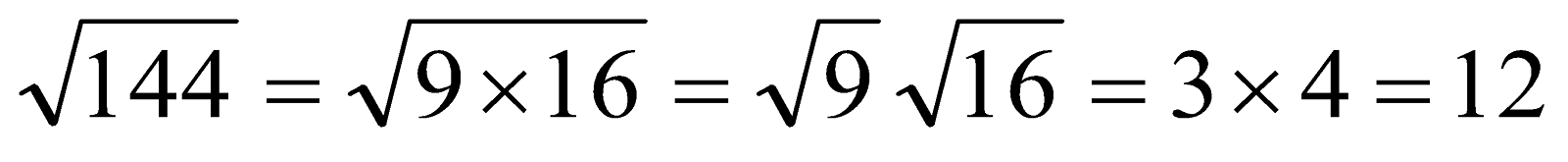
The square root of 144 is 12.
You probably already knew that 122 = 144, so obviously the square root of 144 must be 12. But my steps above show how you can switch back and forth between the different formats (multiplication inside one radical, versus multiplication of two radicals) to help in the simplification process.
-
Simplify
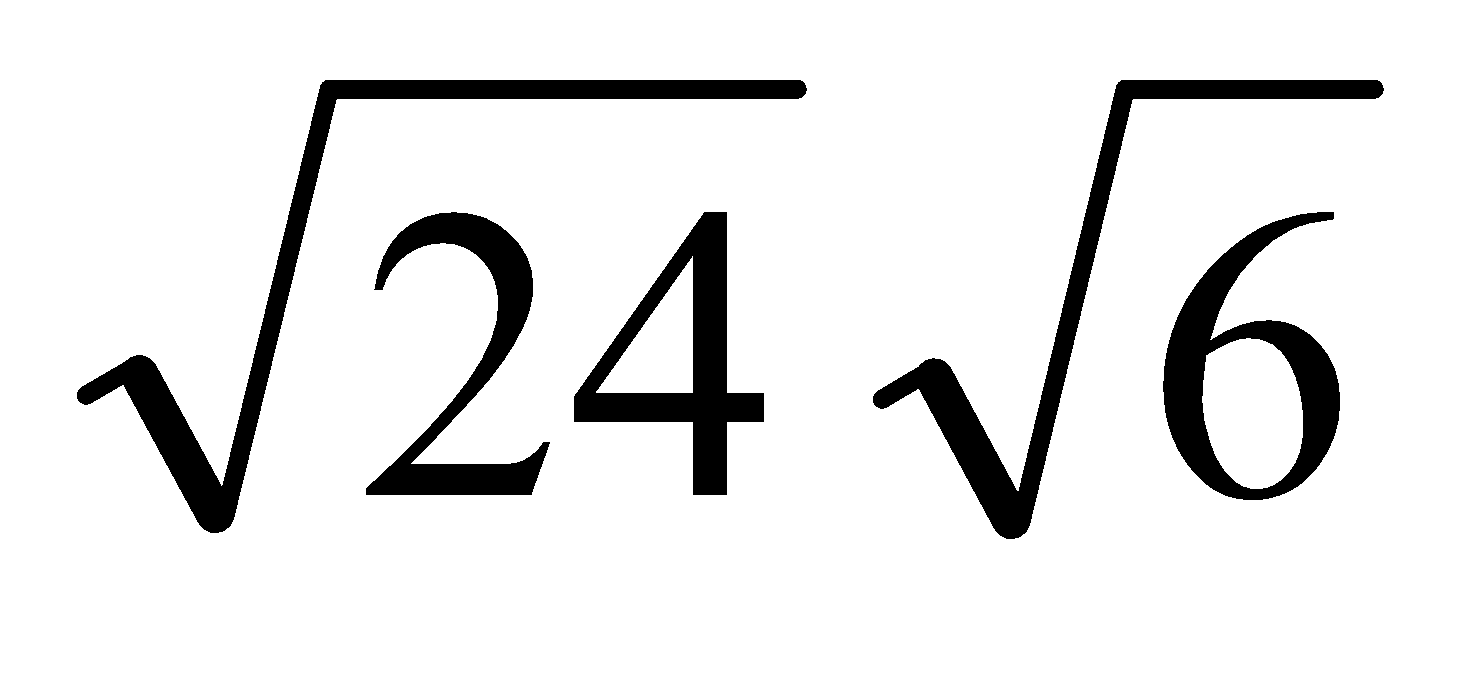
Neither of 24 and 6 is a square, but what happens if I multiply them inside one radical?
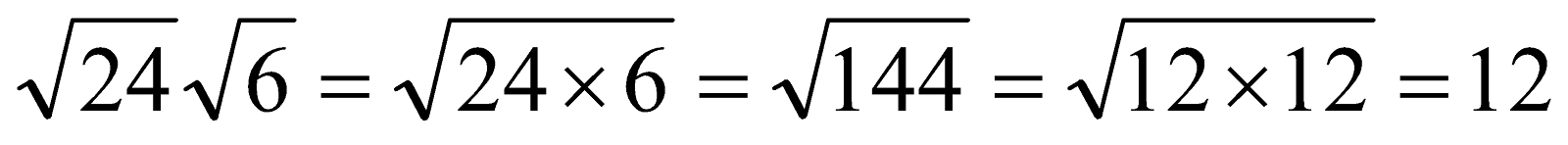
-
Simplify

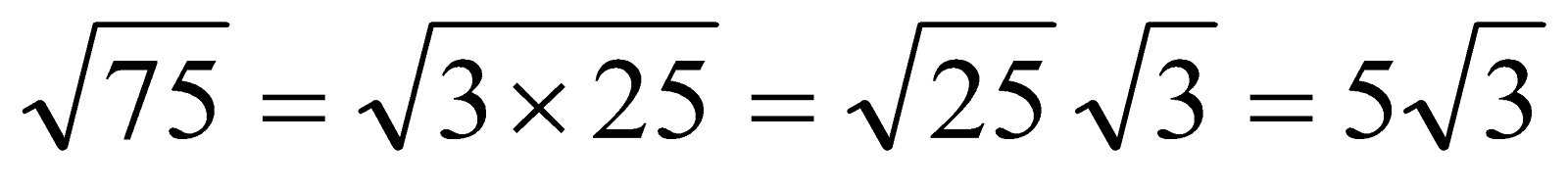
This answer is pronounced as "five, root three". It is proper form to put the radical at the end of the expression. Not only is "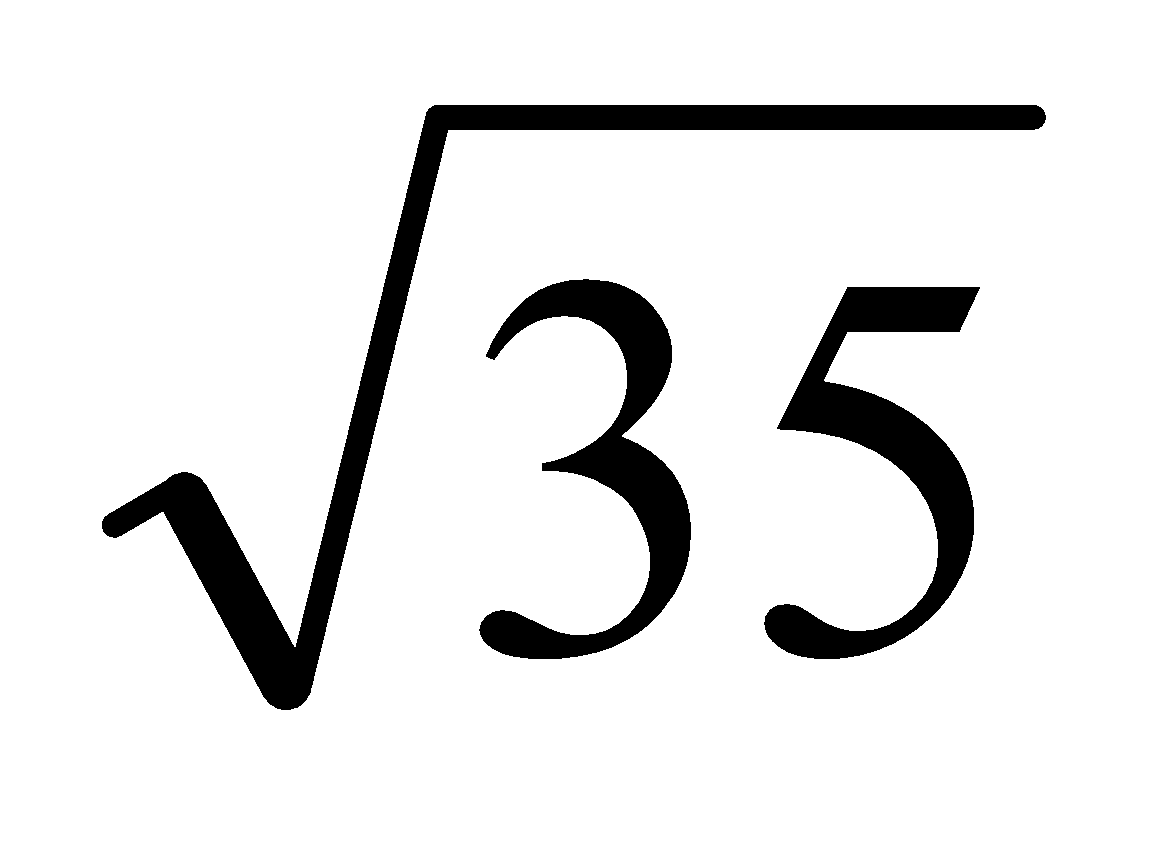 " non-standard, it is very hard to read, especially when hand-written. And write neatly, because "
" non-standard, it is very hard to read, especially when hand-written. And write neatly, because "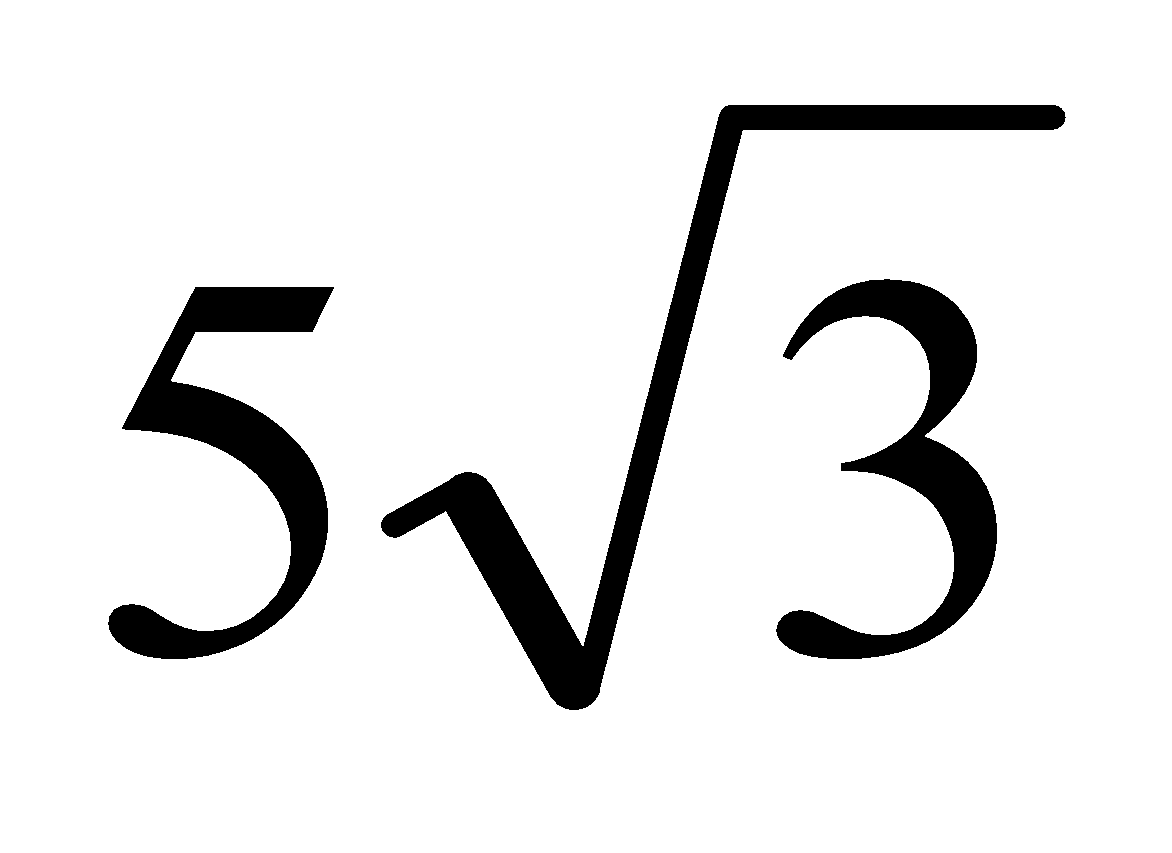 " is not the same as "
" is not the same as "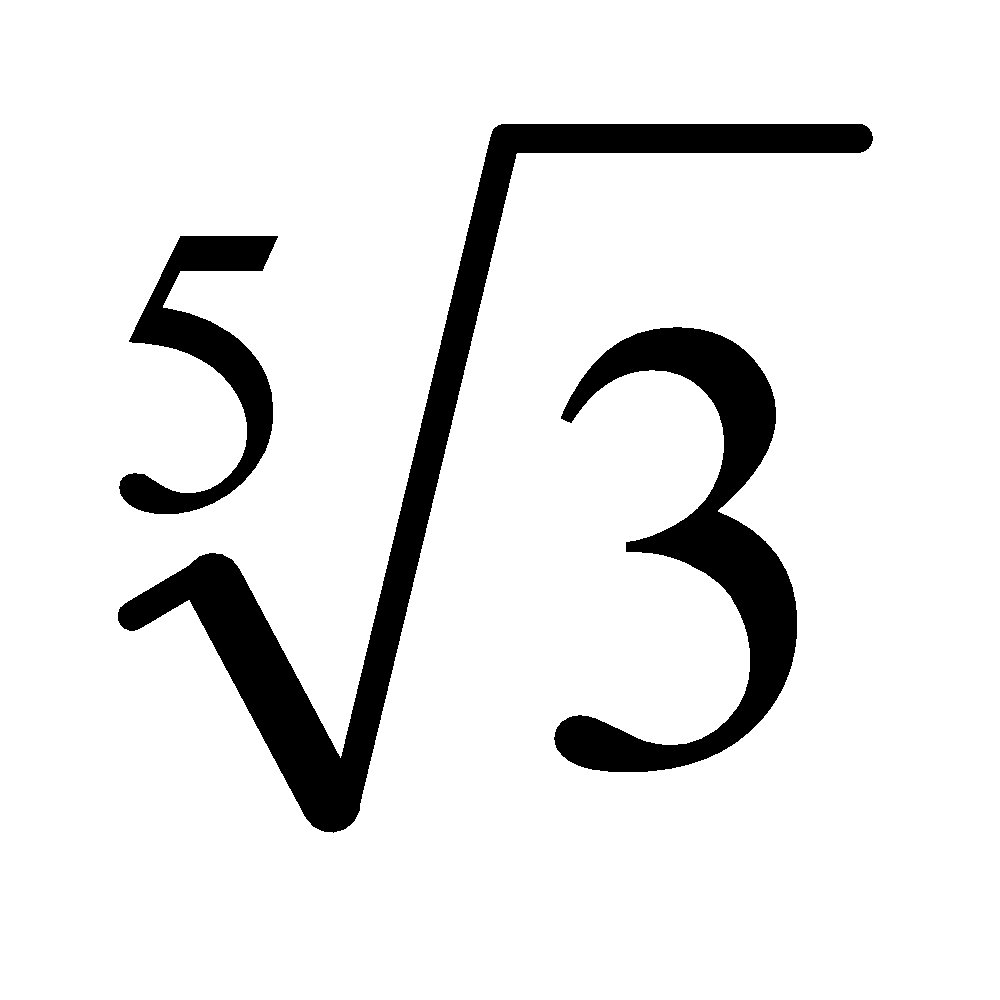 ".
".
You don't have to factor the radicand all the way down to prime numbers when simplifying. As soon as you see a pair of factors or a perfect square, you've gone far enough.
-
Simplify
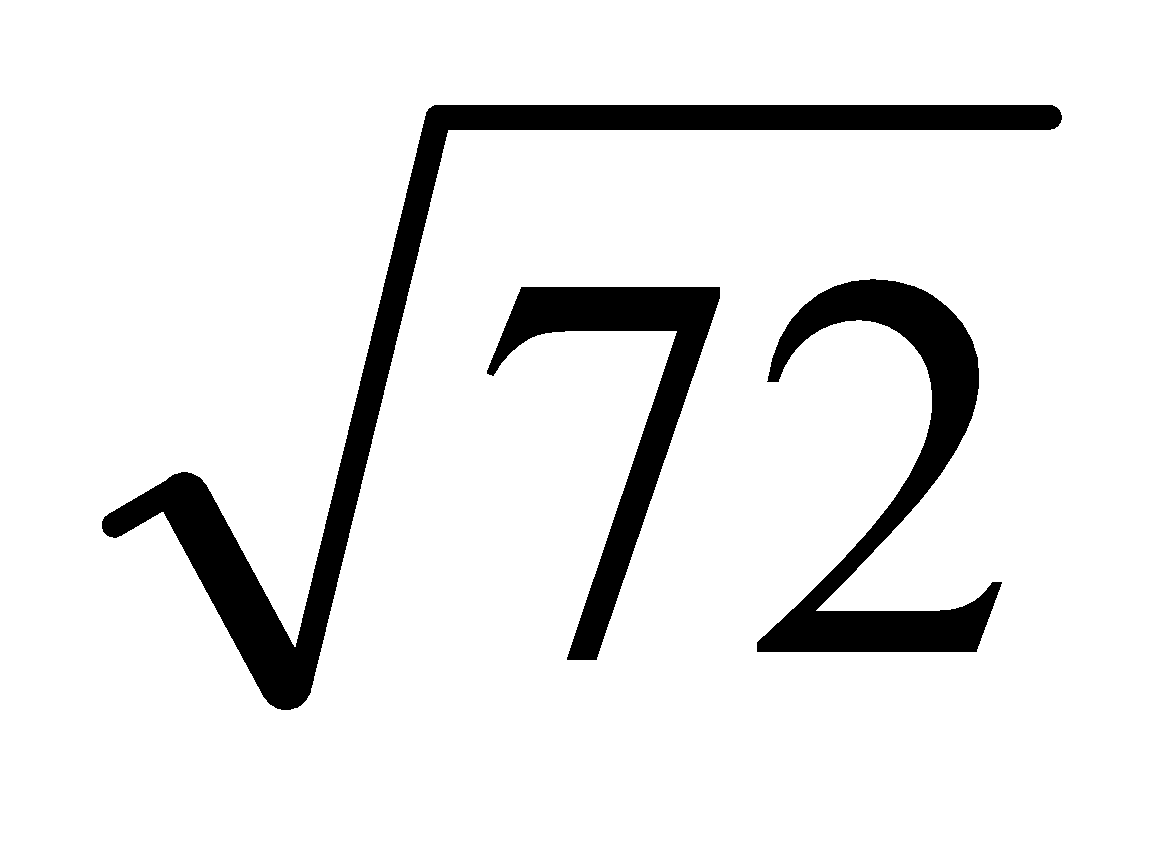
Since 72 factors as 2×36, and since 36 is a perfect square, then:
.png)
Since there had been only one copy of the factor 2 in the factorization 2×6×6, that left-over 2 couldn't come out of the radical and had to be left behind.
-
Simplify
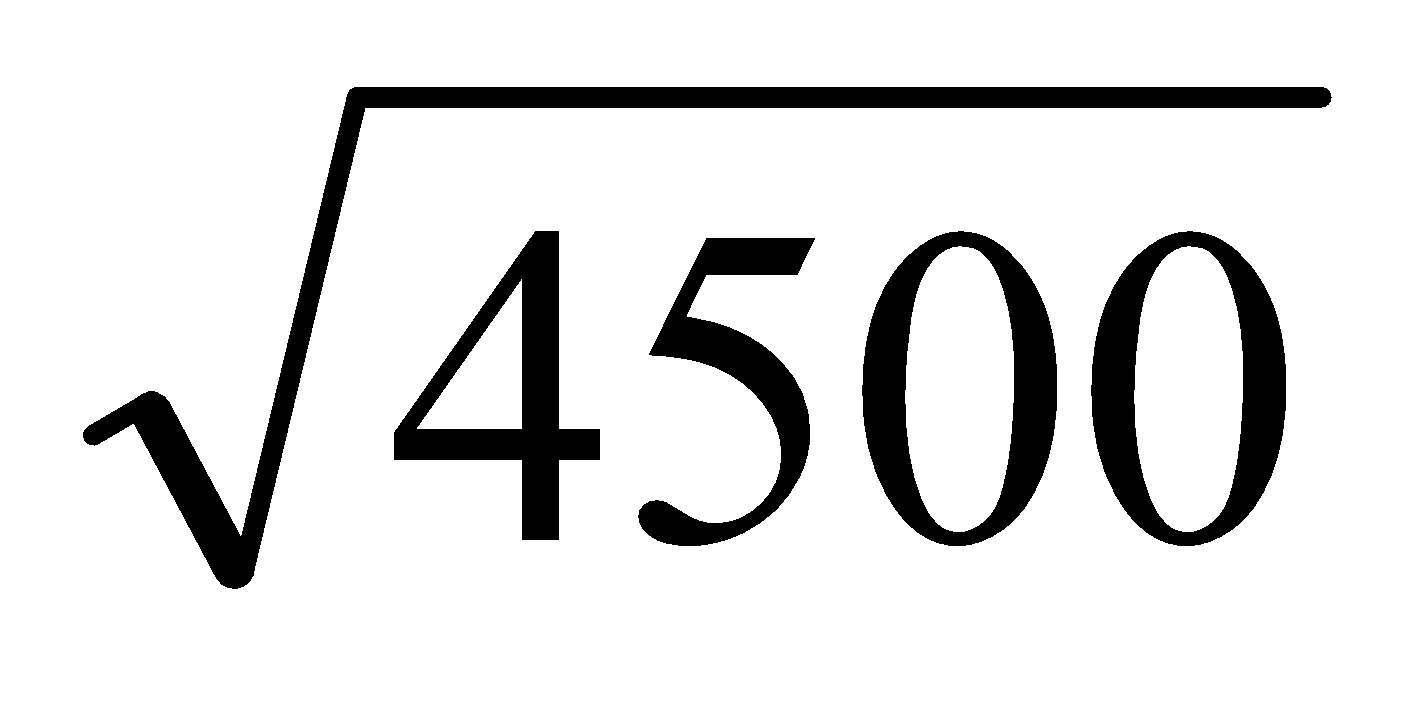
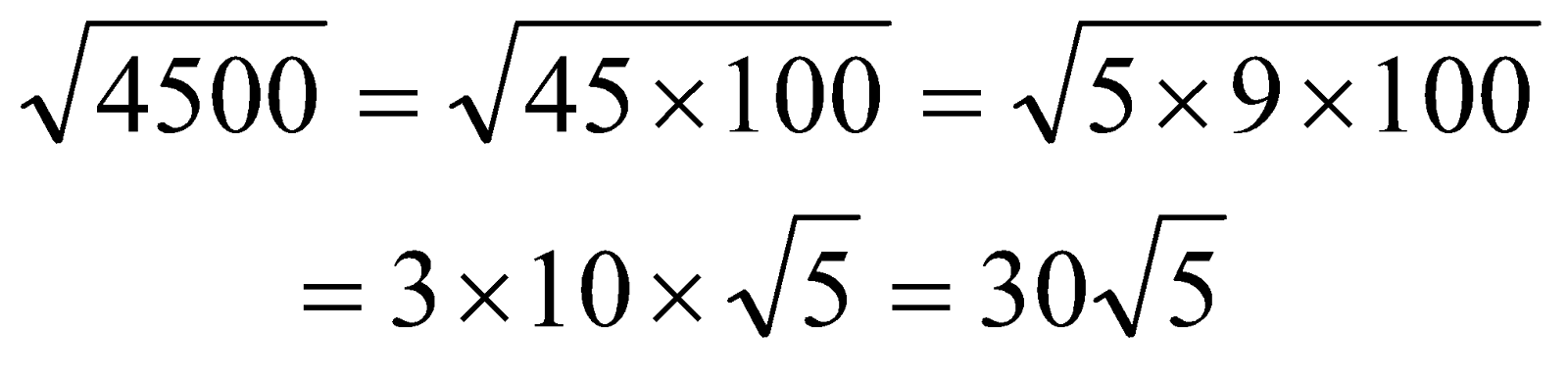
CBSE NCERT Solutions for Class 8 Maths
class 8 maths NCERT solutions Chapter 1: Rational Numbers
class 8 maths NCERT solutions Chapter 2: Linear Equations in One Variable
class 8 maths NCERT solutions Chapter 3: Understanding Quadrilaterals
class 8 maths NCERT solutions Chapter 4: Practical Geometry
class 8 maths NCERT solutions Chapter 5: Data Handling
class 8 maths NCERT solutions Chapter 6: Square and Square Roots
class 8 maths NCERT solutions Chapter 7: Cube and Cube Roots
class 8 maths NCERT solutions Chapter 8: Comparing Quantities
NCERT Class 8 Maths solution Chapter 9: Algebraic Expressions and Identities
class 8 maths NCERT solutions Chapter 10: Visualizing Solid Shapes
class 8 maths NCERT solutions Chapter 11: Mensuration
class 8 maths NCERT solutions Chapter 12: Exponents and Powers
class 8 maths NCERT solutions Chapter 13: Direct and Inverse Proportions
class 8 maths NCERT solutions Chapter 14: Factorization
class 8 maths NCERT solutions Chapter 15: Introduction to Graphs
class 8 maths NCERT solutions Chapter 16: Playing with Numbers
Notes,worksheet and solved question for Maths class 8
- class 8 maths notes on chapter Liner equation in one variable
- class 8 maths notes on chapter algebric expression
- class 8 maths notes on chapter Mensuration
- class 8 maths notes on chapter Square and square roots
- class 8 maths notes on chapter statistice
- class 8 maths notes on chapter practical Geometry
- class 8 maths notes on chapter commericial maths
- class 8 maths notes on chapter solid shape
- class 8 maths notes on chapter quadrilaterals
- class 8 maths notes on chapter exponents
- class 8 maths notes on chapter factorisation
- class 8 maths notes on chapter inverse proporation
- class 8 maths notes on chapter cube and cube roots
Check your marks in a chapter which you have complited in school from Physics Wallah chapter wise online test just click on the link given below










