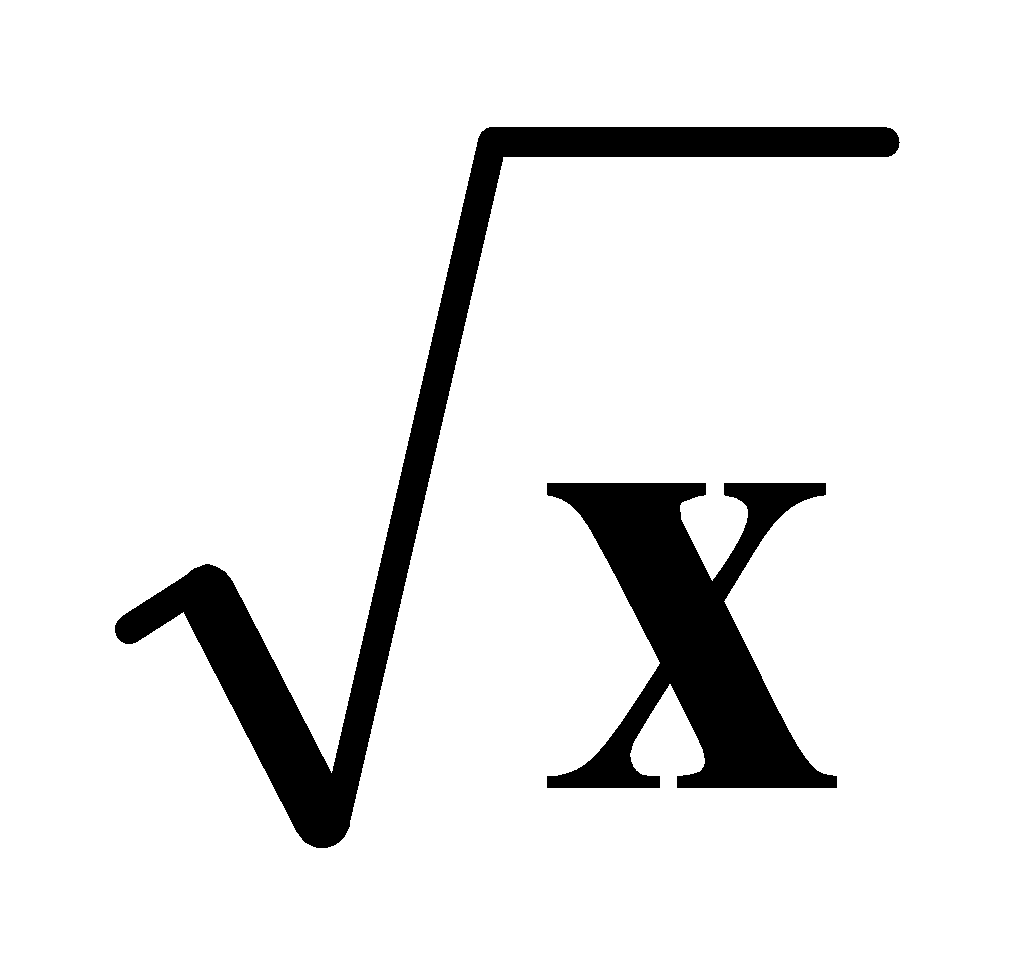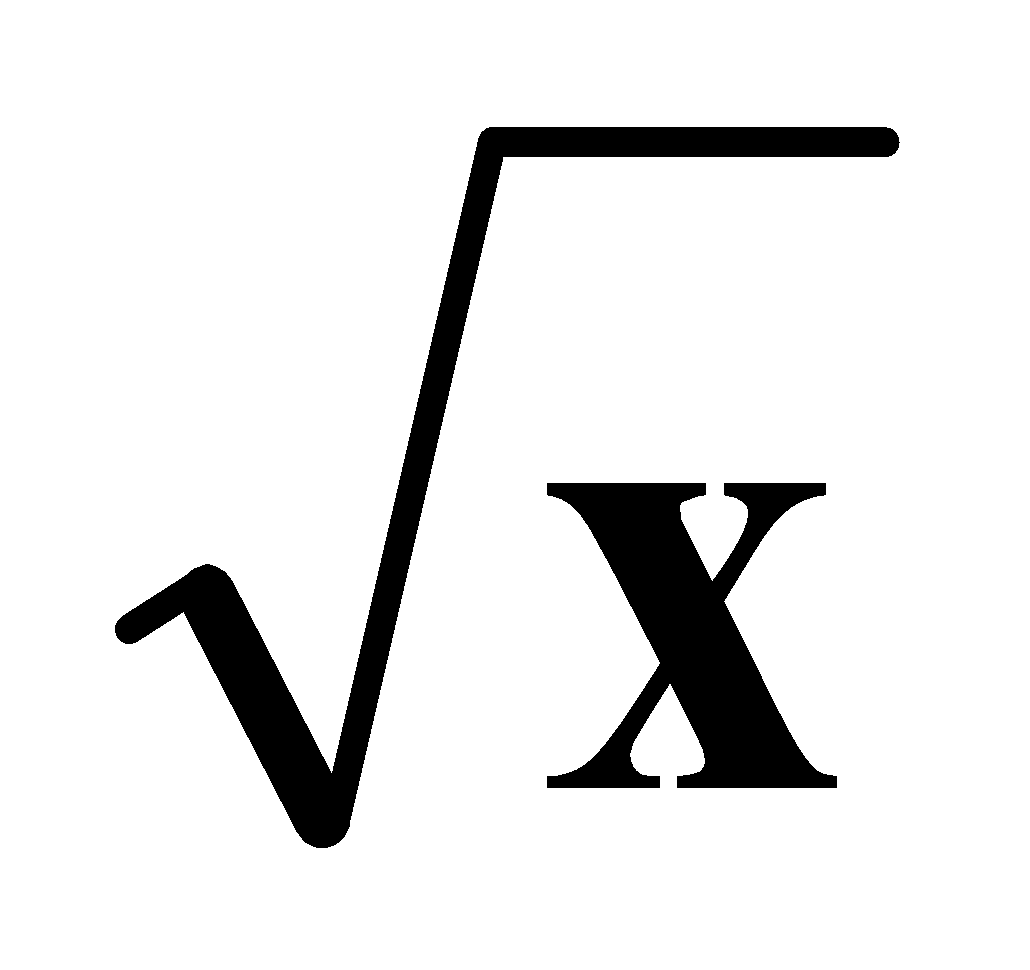SQUARE ROOTS BY LONG DIVISION METHOD

• Obtain the number whose square root is to be computed.
• Place bars over every pair of digits starting with unit digit. 

For example:

• Think of the largest number whose square is less than or equal to the first pair. Take this number as the divisor and the quotient.
• Put the quotient above the period and write the product of divisor and quotient just below the first period.
• Subtract the product of quotient and divisor.
• Bring down the second period on the right of the remainder. This is the new dividend.
• Double the quotient and write this number on the left of the remainder as shown with a blank on the right for the next digit as the next possible divisor.
• Enter a new digit to fill the blank and also as the new digit in the quotient such that the product of this new digit in the quotient with the new divisor is less than or equal to the new divisors.
• Subtract and bring down the next period (if any).
• Repeat the above two steps till all bars have been considered, the final quotient is the required square root.

e.g. Finding the square root of 40: 

The answer is 6.324 . . . taking the method as far as three decimal places.
Notice the position of the decimal point and step away from there in both directions, two digits at a time. Each of those pairs will lead to one digit of the answer, and remember the zeros continue indefinitely. 

Start on the left. The first pair is 40. Find the largest square smaller than 40, that's 36. Subtract the 36 from the 40, which leaves 4, and enter a 6 as the first digit of your answer. 

Next take the 4 and 'bring down' the next pair of digits (00 as it happens) to make 400. We are trying to decide the second digit of our answer and we find it like this: 

Use the 6 but double it (12) and make that ten times bigger (120). Now find 'something'- a single digit, so that one hundred and twenty 'something' times that same 'something' is as large as possible but less than the 400. 

123 times 3 makes 369, so three is the digit we want (124 times 4 would have been too big). 

Subtract the 369 from the 400 (31) and 'bring down' the next pair of digits (so we are now aiming for 3100). The digits we have so far in the answer are 6 and 3. Double 63 and then make it ten times bigger (1260). Use the same technique as before: find one thousand two hundred and sixty 'something', times 'something', that gets as close as possible to 3100 without exceeding it. 

Our third digit will be 2, 1262 times 2 is 2524, 1263 times 3 would be too large. 

Subtract to leave 576, bring down the next pair of digits, double the digits you already have, that's 632, which doubles to make 1264, now look for twelve thousand, six hundred and forty 'something' times 'something' to come as close as possible to 57,600 without exceeding it. That 'something' is 4 (check it), and so we continue until we have as many digits in our answer as we think we need.

APPROXIMATE VALUES OF SQUARE ROOTS BY USING SQUARE ROOT TABLES:

In our practical problems, we need the square roots of numbers. Square roots of numbers by the method of long division is very time consuming and cumbersome. For this reason, tables have been prepared which provide the approximate values of square roots of different numbers correct to a certain decimal place.

The following table gives the values of square roots of all natural numbers from 1 to 99.