Conformation Of Butane
GOC of Class 11
Conformation Of Butane
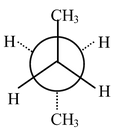
The study of the relative energies of conformational isomers can be done nicely taking butane as an example. Let us have a Newmann projection by looking down the
C(2) − C(3) bond of butane.
|
Let us assume that relatively large methyl groups will best be kept as far from each other as possible then we have the conformation called the anti form shown in fig. (A). 120° clockwise rotation passes over a transition state to a new minimum energy conformation of butane shown in fig. (B). |
Fig (A) |
|
Conformation (B) will be less stable than (A) because in (B) the two methyl groups are closer than they are in (A). Conformation (2) is called ‘gauche’ form. Gauche form of butane (B) is about 0.6 kcal mol−1 higher in energy than the anti form (A). There was an eclipsed transition state for the interconversion of (A) to (B) which lies about 3.4 kcal mol−1 higher |
Fig (B) |
|
Another 120° clockwise rotation brings us to a second gauche form of butane (B). The transition state for the conversion of (B) to (B’) involves an eclipsed state of two |
Fig (B’) |
|
Fig (C) |
|
The angle versus energy plot for butane can be shown as.
Optical Isomerism
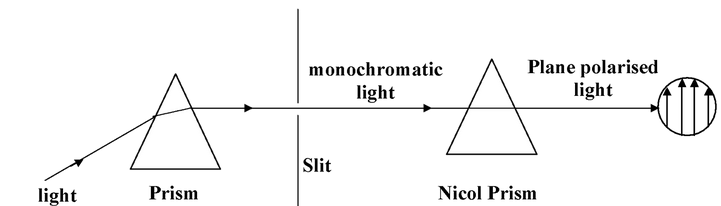
Plane Polarised light
Light contains radiations of different frequencies (wavelengths) which can be separated with the help of prism. The light having radiations of only one frequency is called monochromatic light. In this monochromatic light the radiations propagate in different planes. If this monochromatic light is passed through a nicol prism (It has characteristic that radiations of only one particular plane can pass through it), the radiations traveling in one plane only can be obtained. The radiations (light) traveling in one plane only is called plane polarized light.
Optical Activity and Chirality
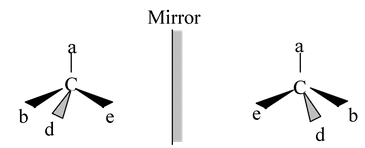
Any compound that rotates the plane polarized light is said to be optically active. If a pure compound is optically active, the molecule is non−superimposable on its mirror image. If a molecule is superimposable on its mirror image, the compound does not rotate the plane of polarized light, it is optically inactive. The property of non−superimposability of an object on its mirror image is called chirality. If a molecule is not superimposable on its mirror image, it is chiral. If it is superimposable on its mirror image, it is achiral. The relationship between optical activity and chirality is absolute, no exceptions are known. The ultimate criterion for optical activity is chirality (non−superimposability of the mirror image). This is both a necessary and a sufficient condition for a compound to exhibit optical activity.
If a molecule is non−superimposable on its mirror image, the mirror image must be a different molecule. In each case of optical activity of a pure compound there are two and only two isomers, called enantiomers (sometimes enantiomorphs), which differ in structure only in the left and right−handedness of their orientations like I and II.
(I) (II)
Physical and chemical properties of enantiomers are as follows.
(1) Enantiomers have identical physical properties like boiling and melting point,
solubility etc.
(2) They rotate the plane of polarized light in opposite directions, though in equal amounts. The isomer that rotates the plane to the left (counterclockwise) is called the laevo isomer and designated (−), while the one that rotates the plane to the right (clockwise) is called the dextro isomer and is designated (+). Because they differ in this property they are often called optical antipodes.
(3) The chemical properties of enantiomers are the same towards achiral reagents, solvents, catalysts, and conditions. Towards chiral reagents, solvents, catalysts, and conditions enantiomers react at different rates. The transition states produced from the chiral reactant and the individual enantiomers are not mirror images. They are diastereomeric, and hence have different enthalpies. The values are different for the two and hence the rates of reaction and the amounts of product formed. Their rates may be so far apart that one enantiomer undergoes the reaction at a convenient rate while the other does not react at all. This is the reason that many compounds are biologically active while their enantiomers are not.
Although pure compounds are always optically active if they are composed of chiral molecules, mixtures of equimolar amounts of enantiomers are optically inactive since the equal and opposite rotations cancel. Such mixtures are called racemic mixtures or racemates. Their properties are not always the same as those of the individual enantiomers.
Different Types of Molecules Displaying Optical Activity
Although the ultimate criterion to know whether a compound will exhibit optical activity or not is the non−superimposability of the mirror image (chirality) but other tests may also be used that are simpler to apply. One such test is the presence of any element of symmetry like plane of symmetry, centre of symmetry and an alternating axis of symmetry.
(i) Plane of symmetry: A plane of symmetry (also called a mirror plane) is a plane passing through the molecule such that the molecule is divided into 2 equals parts, one part being the mirror image of other (the plane acting as a mirror). For example,

Such an isomer is called meso isomer which is optically inactive due to the presence of plane of symmetry.
(ii) Centre of symmetry: A center of symmetry is a imaginary point within the molecule such that a straight line drawn from any part or element of the molecule to the center and extended an equal distance on the other side encounters an equal part or element. For example, 2,4−dimethyl cyclobutane−1,3−dicarboxylic acid possess a centre of symmetry which is the centre of the ring.
Another important example of the compound having a centre of symmetry is the trans form of dimethyl keto piperazine. The compound exists in two forms−cis and trans. The cis form has no element of symmetry and hence exists in two enantiomeric forms but on the other hand the trans−form has a centre of symmetry and therefore, it is optically inactive.
Similarly α−truxillic acid is optically inactive because of the presence of a centre of symmetry.
It must be noted that only even−membered rings can possibly possess a centre of symmetry.
Optically active compounds may be classified into several categories.
(i) Compounds with a chiral carbon atom: If there is only one such atom, the molecule must be optically active. This is so no matter how slight the differences are among the four groups. For example, optical activity is present in
Optical activity has been detected even in cases such as 1−butanol−1−d, where one group is hydrogen and another is deuterium.
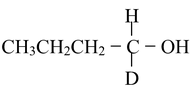
However, the amount of optical rotation is greatly dependent on the nature of the four groups, in general increasing with increasing differences in polarizabilities among the groups. Alkyl groups have very similar polarizabilities and the optical activity of 5−ethyl−5−propylundecane is too low to be measurable at any wavelength between 280 and 580 nm.
(ii) Compounds with other quadrivalent chiral atoms: Any molecule containing an atom that has four bonds pointing to the corners of a tetrahedron will be optically active if the four groups are different. Among atoms in this category are Si, Ge, Sn and N (in quaternary salts or N−oxides),
S and P. In sulfones the sulfur bonds tetrahedrally, but since two of the groups are always oxygen, no chirality normally results. However, the preparation of an optically active sulfone (I) in which one oxygen is 16O and the other 18O illustrates the point that slight differences in groups are all that is necessary. This has even been reflected in the ester (II) and phosphates (III), both of which are optically active.
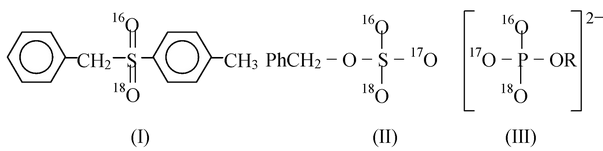
Fischer Projections
When we attempt to depict configurations of a chiral centre, we face the problem of representing three dimensional structures on a two dimensional surface. To overcome this difficulty we use the so-called Fischer projections. This is the structure of an asymmetric carbon atom drawn in a prescribed orientation and then projected into a planar surface.
Thus planar formulas of the asymmetric carbon are obtained by placing it so that the two substituents are horizontal and project towards the viewer (shown by thick wedge-like bonds), while the two other substituents are vertical and project away from the viewer (shown by dotted bonds). Hence we may draw the two configurations of lactic acid by
Fischer projection as
In these formulas the horizontal bonds i.e., C–OH and C–H project towards us out of the plane of the paper whereas the vertical bonds i.e., C–COOH and C–CH3 project away from us. Furthermore, since the vertical bonds are actually behind the plane of the paper, the formula may be rotated by an angle of 180o (not by 90o or 270o). Inspection of the models shows that odd interchange of a pair of substituents inverts the configuration (changes one enantiomer into its mirror image), whereas even number of such interchanges does not preduce enantiomer. Thus interchanging of –H for –OH in I gives the enantiomer II, while the interchange of CH3 for –COOH and–H for –OH leaves the configuration unchanged.
Relative Configuration
While discussing optical isomerism, we must distinguish between relative and absolute configuration (arrangement of atoms or groups) about the asymmetric carbon atom. Let us consider a pair of enantiomers, say (+) and (–) lactic acid.
We know that they differ from one another in the direction in which they rotate the plane polarised light. In other words, we know their relative configuration in the sense that one is of opposite configuration to the other. But we have no knowledge of the absolute configuration of the either isomer. That is, we cannot tell as to which of the two possible configuration corresponds to (+) - acid and which to the (–) - acid. A given isomer is dextro or laevo, can only be known using optical measurements. If compounds rotates the plane polarized light in clockwise direction, it is dextro otherwise laevo isomer.
D and L system
The sign of rotation of plane-polarized light by an enantiomer cannot be easily related to either its absolute or relative configuration. Compounds with similar configuration at the asymmetric carbon atom may have opposite sign of rotations and compounds with different configuration may have same sign of rotation. Thus d-lactic acid with a specific rotation + 3.82° gives l-methyl lactate with a specific rotation -8.25°, although the configuration (or arrangement) about the asymmetric carbon atom remains the same during the change.

Obviously there appears to be no relation between configuration and sign of rotation.
Thus D-L-system has been used to specify the configuration at the asymmetric carbon atom. In this system, the configuration of an enantiomer is related to a standard, glyceraldehyde. The two forms of glyceraldehyde were arbitrarily assigned the configurations as shown below.
If the configuration at the asymmetric carbon atom of a compound can be related to D (+)-glyceraldehyde, it belongs to D-series and if it can be related to L(–)-glyceraldehyde, the compound belongs to L-series. Thus many of the naturally occurring α-amino acids have been correlated with glyceraldehyde by chemical transformations. For example, natural alanine (2-aminopropanoic acid) has been related to L(+)-lactic acid which is related to L(–)-glyceraldehyde. Alanine, therefore, belongs to the L-series.
In general, the relative configuration of a substituent (X) at the asymmetric centre is specified by writing the projection formula with the carbon chain vertical and the lowest number carbon at the top. The D configuration is then the one that has the substituent 'X' on the bond extending to the 'right' of the asymmetric carbon, whereas the L configuration has the substituent 'X' on the 'left'.
Thus,
When there are several asymmetric carbon atoms in a molecule, the configuration at one centre is usually related directly or indirectly to glyceraldehyde. In the configurations of the natural (+)-glucose there are four asymmetric centres (marked by asterisk). By convention for sugars, the configuration of the highest numbered asymmetric carbon is related to glyceraldehyde to determine the overall configuration of the molecule. For glucose, this atom is C–5 and therefore, OH on it is to the right. Hence the naturally occurring glucose belongs to the D-series and is named as D-glucose. Must naturally occuring carbohydrates have the D−configuration.
However, the above system of nomenclature based on Fischer projection formula, has certain disadvantages. Firstly before a name can be assigned to a compound, we must specify how its projection formula is oriented.
Secondly, sometimes the two asymmetric carbon atoms having the same kind of arrangements of substituents are assigned opposite configurational symbols. As in (−) 2,3−dichlorobutane.
Erythro and threo terms are used to describe diastereomers with two chiral C's (usually adjacent) when both C's have two sets of identical ligands. In 3−chloro−2−butanol, the identical ligands are H and Me. When the different ligands, in this case OH and Cl are on the same side of the vertical bonds as in fig (a), the molecule is called erythro (related to the sugar erythrose). When they are on opposite sides as in fig (b), the molecule is called threo (related to the sugar threose). The relationship of the erythro to a meso structure is apparent if we change OH to Cl.
Optical isomerism in compounds with more than one asymmetric carbon atom
In the above discussion we have seen that an asymmetric carbon atom can produce molecular asymmetry. Thus the molecules containing an asymmetric carbon exist in two optically active forms, (+)-isomer and (–)-isomer, and an equimolar mixture of the two which is called (±)-mixture, is optically inactive. When there are two or more asymmetric carbon atoms in a molecule, the problem is complicated considerably.
An organic compound which contains two dissimilar asymmetric carbons, can give four possible stereoisomeric forms. Thus 2-bromo-3-chlorobutane may be written as
The two asymmetric carbons in this molecule are dissimilar in the sense that the groups attached to each of these are different.
C2 has CH3, H, Br, CHClCH3
C3 has CH3, H, Cl, CHBrCH3
Such a substance can be represented by four isomers in Fischer projection.
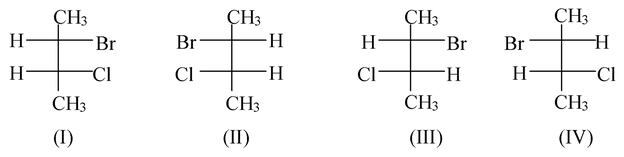
The forms I and II are optical enantiomers (related as object and mirror image) and so are forms III and IV. These two pairs of enantiomers will give rise to two possible racemic modifications.
It may be noted that forms I and III are not mirror images or enantiomers, and yet they are optically active isomers. Similarly, the other two forms i.e., II and IV are also not enantiomers but optically active isomers.
Such stereoisomers which are optically active isomers but not mirror images, are called Diastereoisomers or Diastereomers.
Number of Optical Isomers
As it has been discussed above, a compound containing two dissimilar carbon atoms can exist in four optically active forms. Reasoning in the same fashion, we will find that a compound containing three such asymmetric carbon atoms can exist in eight different configurations which represent optical isomers. Thus in general, the number of stereoisomers for a compound with n distinct (different) asymmetric carbon atoms is .
When an organic compound contains two similar asymmetric carbon atoms in its molecule, abd C–Cabd, the number of optically active isomers decreases. Thus tartaric acid [HO2CCH(OH)CH(OH)CO2H] has two similar asymmetric carbon atoms and exists in only three forms (optical isomers), of which two are optically active and one is optically inactive (meso form). Thus the general guidelines for predicting the number of optical isomers is given as under.
1. When the molecule is unsymmetrical
Number of d and l isomers (a) =
Number of meso forms (m) = 0
∴ Total number of opical isomers (a + m) =
Where n is the number of chiral carbon atom(s).
Common example is CH3CHBrCHBrCOOH
2. When the molecule is symmetrical and has even number of chiral carbon atoms.
Number of d and l isomers (a) =
Number of meso forms (m) =
∴ Total number of optical isomers = (a + m)
Common example is tartaric acid, HOOCCHOHCHOHCOOH
3. When the molecule is symmetrical and has an odd number of chiral carbon atoms.
Number of d and l forms (a) =
Number of meso forms (m) =
∴ Total number of optical isomers = (a + m) =
CH3CHOHCHOHCHOHCH3
Isomerism of Tartaric Acid
Let us now proceed to discuss the optical isomerism of tartaric acid which contains two similar asymmetric carbon atoms, in detail.
The two asymmetric carbon atoms in tartaric acid,
*CH(OH)COOH
*CH(OH)COOH
are attached to the groups H, OH, COOH and CH(OH)COOH. The end groups being identical, four arrangements are possible as one or both H groups and OH groups, are on the left or on the right. These arrangements are shown by Fischer projections.
Of these, formula (IV) when rotated through 180° in the plane of the paper becomes identical with formula III. Therefore, for tartaric acid we can have only three different arrangements, viz. (I), (II) and (III).
Structure III will represent optically inactive tartaric acid, since it has a plane of symmetry. The optical rotation of the upper half of the molecule is balanced by that of the lower half.
It may also be noted that formulae I and II are mirror images of each other and thus one of them is dextro and the other is laevo. Formula III, however represents an inactive isomer of tartaric acid called meso form.
In actual practice, four types of tartaric acids are known.
(i) (+)-Tartaric acid
(ii) (–)-Tartaric acid
(iii) Inactive or i-tartaric acid (this is also known as meso-tartaric acid or m-tartaric acid).
(iv) (±) Tartaric acid (this form of tartaric acid being a mixture of equal amounts of
(+)- and (–)-isomers).
The physical properties of the four tartaric acids are tabulated as
|
Name |
Melting point(°c) |
Density (g/cc) |
Optical rotation |
|
(+)-Tartaric acid |
170 |
1.760 |
+12° |
|
(–)-Tartaric acid |
170 |
1.760 |
-12° |
|
(±)-Tartaric acid |
206 |
1.697 |
0° |
|
m-Tartaric acid |
140 |
1.666 |
0° |
The three tartaric acids, (+)-, (–)-, m-, are all space isomers but m-tartaric acid is not a mirror image of either of the active forms. Hence it differs from them in melting point, density and other physical properties.
External and Internal Compensation
If equimolecular amounts of d- and l-isomers are mixed in a solvent, the solution is inactive. The rotation of each isomer is balanced or compensated by the equal but opposite rotation of the other. Optical inactivity having this origin is described as due to External Compensation.
|
Such mixtures of (+)- and (-)- isomers (Racemic mixtures) can be separated into the active components. In meso tartaric acid the inactivity is due to effects within the molecule and not external. The optical rotation due to one half of the molecule is balanced by the opposite and equal optical rotation due to the other half. The optical inactivity so produced is said to be due to internal compensation. It occurs whenever a compound containing two or more asymmetric carbon atoms has a plane or point of symmetry. Since the optical inactivity of such a compound arises within the molecule, the question of separating into active components does not arise. |
Inactivity of Meso Tartaric acid by Internal Compensation. |
Geometrical Isomerism
The sufficient and necessary conditions for a compound to show geometrical isomerism are
(a) There must be restricted rotation in the molecule either due to C = C, C = N, N = N, C = S bonds or alicyclic compounds.
(b) The atoms or group of atoms attached to each doubly bonded carbon must be different.
These compound do not rotate the plane polarized light (unless they happen to be chiral), and the properties of the isomers are not identical.
In the given compound, the two carbon atoms of C = C double bond and the four atoms directly attached to them are all in the same plane and that rotation around the double bond is prevented. This means that in the case of a molecule wx C = C y z, stereoisomerism exists when w ≠ x and y ≠ z. There are two isomers I and II, each superimposable on its mirror image unless one of the groups happens to carry a chiral centre. Note that the I and II are diastereomers.
In the present case the isomer in which same groups are on same sides of the two carbon atoms, is called cis isomer and the one in which the same groups are on opposite side of the two carbon atoms, is called trans isomer.
It may be noted that cis and trans nomenclature can not be applied in those cases when the four groups are different. For such cases, the E and Z nomenclature system proposed by Cahn−Ingold and Prelog is followed which is not included in the syllabus of IIT−JEE.
For example
Here, we can not use cis and trans isomerism because all four groups attached to C = C are different, thus E −Z nomenclature is applicable to them.
Geometrical isomerism is also possible with other double bonds such as C = N, N = N, or even C = S, though in these cases only two or three groups are connected to the doubly bonded atoms. In case of imines, oximes and other C = N compounds if w = y, III may be called syn and IV may be called anti. In azo compounds, there is no ambiguity, V is always syn regardless of the nature of w and y.
The presence of a ring, like that of a double bond, prevents free rotation. Cis and trans isomers are possible whenever there are two carbons on a ring, each of which is substituted by two different groups. The two carbons need not be adjacent. For example,
As with double bonds, w may equal y and x may equal z, but w may not equal x and y may not equal z if cis and trans isomers are to be possible. There is an important difference from the double−bond cis−trans isomerism. The substituted carbons are chiral carbons. This means that there are not only two isomers. In the most general case, where w, x, y and z are all different, there are four isomers since neither the cis nor the trans isomer is superimposable on its mirror image. This is true regardless of ring size or which carbons are involved, except that in rings of even−numbered size when w, x, y and z are at opposite corners, no chirality is present.
Number of Geometrical isomers
(i) When only one double bond is present in the molecule, the number of geometrical isomers are 2n where n = number of double bonds for molecules having identical ends as well as for molecules having different ends. For example, 2−butene having 1 double bond and similar ends have 2 isomers.
and 2−pentene having 1 double bond and different ends also have 2 isomers.
(ii) If a compound has 2 or more double bonds and ends are different, then the number of geometrical isomers are where n = number of double bonds. For example, 2,4−heptadiene has 4 isomers.
For example,
2,4,6−nonatriene has 3 double bonds and ends are different, therefore number of geometrical isomers are 23 = 8 isomers.
(iii) If a compound has 2 or more double bonds and ends are identical, then the number of geometrical isomers are .
where p = n/2 when number of double bonds are even. (n = Number of double bonds)
and p = when number of double bonds are odd.
For example, 2,4−hexadiene having 2 double bonds and identical ends have only
3 geometrical isomers.
Note: cis−trans and trans−cis are same isomers. Therefore, in all there are three geometrical isomers.
(iv) When a molecule contains a double bond and an asymmetric carbon, there are four isomers, a cis pair of enantiomers and a trans pair of enantiomers.
Stability of Cis, Trans or Geometrical isomers
|
The trans isomer of alkenes are usually more stable than their corresponding cis isomer. The reason for this becomes clear if we consider the cis and trans isomers of the alkene wxC= Cwx in which 'w' is a bulky group as compared to 'x' (e.g., CH3–HC=CH–CH3). In the cis isomer, the two bulky 'w' groups are very close to each other. The steric repulsion due to the overlapping of the electron clouds of the two bulky 'w' groups will make this isomer less stable than trans isomer in which the bulky 'w' groups are far apart (being on the opposite sides of the double bond). |
cis isomer trans isomer The bulky 'w' groups in the cis isomer being very near will overlap, while in the trans isomer the 'w' groups lie far apart and do not overlap. |
Determination of Configuration of Isomers from study of their Physical Properties
There is no absolute method for the determination of the configuration of cis and trans isomers. Several elementary relationships are, however, helpful for the beginners.
The difference in the structure of cis and trans isomers is reflected in their physical properties. Some such properties are illustrated below.
(1) Dipole Moments: The trans isomers have normally less dipole moments than their corresponding cis isomers. The reason for this is clearly understood if we consider the cis and trans isomers of 1,2-dichloroethylene. The trans isomer has a dipole moment of zero. This is due to the fact that the two bond moments of C–Cl bonds are opposed because of the symmetry of the molecule. On the other hand, the cis isomer being non-symmetrical has a definite dipole moment because here the bond moments are not opposed.
In such alkenes which have one polar substituent different from the other, the dipole moment will not normally be zero but would be smaller than the corresponding cis isomer. However if one of the substituent is electron-donating and the other is electron-withdrawing, the bond moments are fully additive in trans isomer. Thus the trans isomer in this case has a higher dipole moment than the corresponding cis isomer.
Therefore, it is possible to assign configuration to a pair of isomers on the basis of dipole measurements, provided the nature of substituents is known to us.
(2) Melting Points and Related Phenomena: In general, a trans isomer has greater symmetry than the corresponding cis isomer. Thus it packs more closely in the crystal lattice and hence has higher melting points. Cis compounds, on the other hand, have low melting points since they being less symmetrical do not pack closely in the crystal lattice. Moreover, the poor packing leads to weaker forces of attraction between the molecules in the crystal lattice. The weaker forces of attraction can be easily broken by the dielectric constant of the solvents and hence the cis isomers have greater solubilities than their trans isomers. cis compounds have also been found to have higher heats of formation and ionization constants as acids. Due to these differences in properties, it is sometimes possible to assign configurations to a pair of geometrical isomers.
(3) By Chemical Methods: The formation of a cyclic molecule from an open chain molecule takes place easily only when the reacting groups are close to each other. This fact has been most useful in assigning configuration to cis-trans isomers in which the doubly bonded carbon atoms carry groups that are capable of reacting with each other. In the configuration of maleic acid, the two −CO2H groups are nearer to each other than they are in fumaric acid i.e.
Obviously maleic acid is the cis form and fumaric acid is the trans form.
In addition to the methods given above, other physical measurements such as the measurement of the distances between certain atoms by means of X-rays, measurement of absorption spectra etc. may be helpful for deciding the configuration in some cases.
Interconversion of Geometrical Isomers
Although geometrical isomers are stable at ordinary temperatures, one can be converted into the other or to an equilibrium mixture of both by heat, by exposure to ultraviolet light, or by the use of catalysts. Thus,
This interconversion of cis to trans isomer involves the breakage of carbon-carbon π−bond. The cleavage of the carbon-carbon π−bond requires approximately 40 kcal/mole of energy. At room temperature, only an insufficient proportions of collisions possesses this energy and hence the rate of interconversion is very slow but can be increased by employing higher temperatures. The interconversion presumably follows the following pathway.